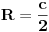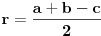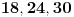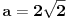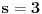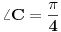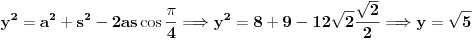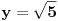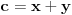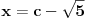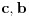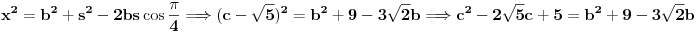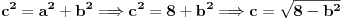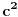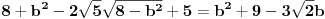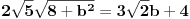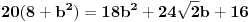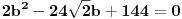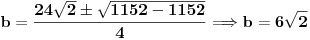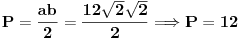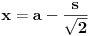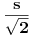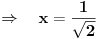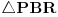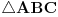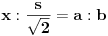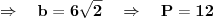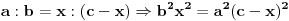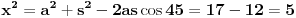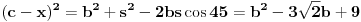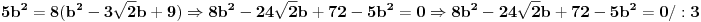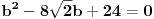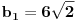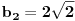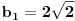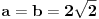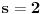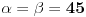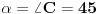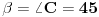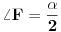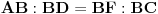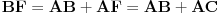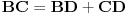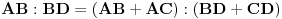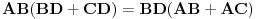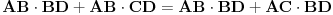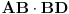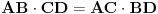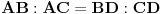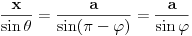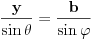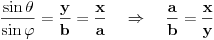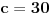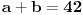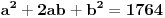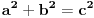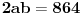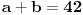|
|
[ zivota11 @ 17.06.2007. 21:37 ] @
|
| U zadatku : Dat je pravougli trougao. Poluprecnik opisanog kruga je R = 15, a poluprecnik upisanog kruga je r = 6. Odredi stranice trougla?
Nadjem hipotenuzu preko c/2sinus90 = 30 ali ne ide dalje??? ako radim preko obrasca (h-6)^2 = (b-15)^2 +225 , a h^2 = b^2 - 225
Da li ovo moze samo u slucaju jednakokrakog trougla ili ??? Dobijem da je b = 15 a to se ne uklapa u resenje?
|
[ Farenhajt @ 17.06.2007. 21:45 ] @
Pođi od dveju poznatih formula za pravougli trougao:
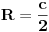
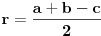
Dobićeš sistem od jedne kvadratne i jedne linearne jednačine po  i  .
Odgovor: 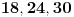 [ wise_monkey @ 17.06.2007. 21:46 ] @
hipotenuza je uvek jednaka prečniku opisanog kruga... a ostale dve stranice nađeš preko pitagorine teoreme i prečnika upisanog kruga
[ zivota11 @ 17.06.2007. 22:18 ] @
Hvala na pomoci, sad je mnogo jasnije...
Ako moze pomoc i oko ovog zadatka?
Jedna kateta pravouglog trougla je a = 2sqrt(2), a duzina simetrale pravog ugla je s = 3 . Odrediti povrsinu trougla?
Dali je ta simetrala = c/2 u pravouglom trouglu?
[ RMAN @ 17.06.2007. 23:06 ] @
Evo ovako:
[att_img]
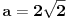 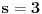 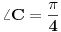
Mozes naci  preko kosinusne teoreme:
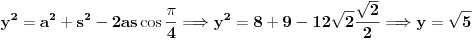
Posto je 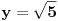 i posto je 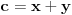 onda je 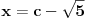
Sada napravis sistem jednacina sa 2 nepoznate 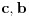 ,pomocu kosinusne teoreme i pomocu pitagorine teoreme:
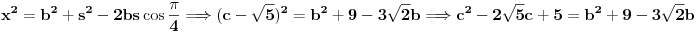
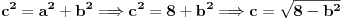
Sada 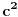 i  iz druge jednacine ubacis u prvu jednacinu:
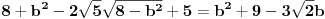
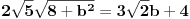 Sada ovo kvadriras
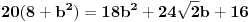
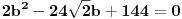
Ova kvadratna jednacina ima samo jedno resenje:
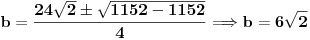
I konacno povrsina:
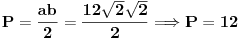
Simetrala pravoug ugla ne deli hipotenuzu na 2 jednaka dela sto se vidi i sa slike.
Ovo verovatno moze i na laksi nacin ali ni ovo nije za bacanje 
[ Daniel011 @ 17.06.2007. 23:54 ] @
Evo još jednog načina, pa možeš da biraš. 
[att_img]
Sa slike se vidi da je 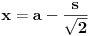 (  je dijagonala kvadrata  , tako da su njegove stranice  )
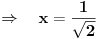
Uočimo sličnost trouglova 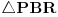 i 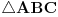 :
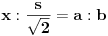
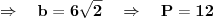 [Ovu poruku je menjao Daniel011 dana 18.06.2007. u 01:12 GMT+1]
[Ovu poruku je menjao Daniel011 dana 18.06.2007. u 01:12 GMT+1][ Kolins Balaban @ 18.06.2007. 01:13 ] @
Svoje rjesenje navodim samo zato da bih spomenuo jednu teoremu, koja se rijetko cuje (bar se meni tako cini), kad je u pitanju planametrija.
Teorema: Simetrala ugla u trouglu dijeli suprotnu stranicu u omjeru stranica koje obrazuju taj ugao.
Napomena za RMANA: Prema tvojim rezultatima, ispade stranica b veca nego sto je stranica a, a na slici nije tako, jer se ne drzis pravila, kad je u pitanju oznacavanje pravouglog trougla. Kod pravog ugla je uvijek vrh C, a desno od njega je vrh A.
Nacrtat cu sliku, koja je po meni ispravna.
Prema navedenoj teoremi, a prema oznakama sa slike, imamo da je:
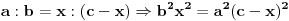 *
Primjenom kosinusne teoreme na trougao BCD, imamo:
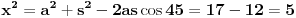 **
Primjenom kosinusne teoreme na trougao ACD, imamo:
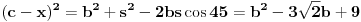 ***
Kad jednacine ** i *** uvrstimo u jednacinu * dobijemo:
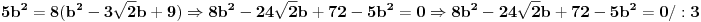
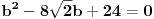
Rjesenja ove jednacine su:
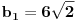 i 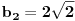
Rjesenje 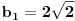 otpada (ako ne skontas zasto, pitaj)
Posto imas a i b, onda povrsinu izracunas onako kako je to RMAN uradio.
Pozz!
[att_img] [ zivota11 @ 18.06.2007. 12:00 ] @
hvala momci na pomoci, RMAN, jel upisujes E2 na FTN?
[Ovu poruku je menjao zivota11 dana 18.06.2007. u 14:00 GMT+1]
[ Daniel011 @ 18.06.2007. 12:32 ] @
Ja ne kontam zašto, može li pojašnjenje? Mislim, jasno je da ne može biti 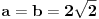 , jer bi tada bilo 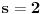 a ne 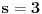 , ali kako direktno iz tvog računa zaključiti da ovo rešenje otpada?
Ne vidim kakve veze označavanje temena na slici ima sa pravilnim odnosom dužina stranica? Ti si, recimo, nacrtao sliku na taj način, da se teme  nalazi desno od temena  , ali i pored toga te ništa nije sprečavalo da stranicu  nacrtaš dužu od  . Ja sliku crtam tako što za vreme crtanja vodim računa (donekle) o brojnim vrednostima dužina stranica, tako da dobijem koliko-toliko korektne proporcije, ali to nema veze sa načinom obeležavanja temena. A čak i ako se ne pridržavamo proporcija, pa dobijemo sliku sa pogrešnim odnosom stranica kao što je slučaj u RMAN-ovom rešenju, to i nije toliko bitno jer ne utiče na dobijeni rezultat.
I mada ovo nema veze sa samom matematikom - za sve koji budu upload-ovali slike - preporučljivo je crteže redukovati na samo 2 boje (belu i crnu), a zatim ih spakovati u GIF-format, na taj način se dobije mnogo manji fajl u kB nego kad se pakuje u JPEG (mada ni JPEG nije preterano veliki), ali i linije su mnogo oštrije, jer nema zamućenja karakterističnog za JPEG-format. [ Kolins Balaban @ 18.06.2007. 13:49 ] @
Vrlo jednostavno, ako bi bilo 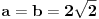 , onda bi za uglove trougla ABC vrijedilo 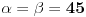
Ako pogledamo sada trouglove ACD ili BCD, vidjet cemo, da i oni imaju po dva ugla od 45° (za trougao ACD 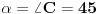 , a za trougao BCD 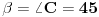 ), pa bi sa slike trebalo da bude, za trougao BCD, x=s, a za trougao ACD je s=c-x (zbog cinjenice, da naspram jednakih uglova, leze jednake stranice, i obratno), a iz dobijenih vrijednost za x i zadate vrijednost s, vidimo da to ne moze biti. [ Daniel011 @ 18.06.2007. 14:33 ] @
Oki, mislio sam da postoji neki direktniji način da se to rešenje odbaci, a nerviralo me što ne mogu da ga uočim. Znači, ipak mora da se upoređuje sa zadatim vrednostima, kao što sam i napisao...
Reci mi, u vezi ove teoreme sa odnosom delova stranice koje deli simetrala, pošto se ranije nisam susretao s njom, ima li ta teorema neki naziv, po kome bih mogao da je pronađem na net-u? Što se dokaza tiče, ja sam je dokazao putem sinusne teoreme u par redova, ima li neki još jednostavniji način dokazivanja?
[ Kolins Balaban @ 18.06.2007. 16:01 ] @
Evo prisjetio sam se dokaza :)
Produzimo stranicu AB, trougla ABC do tacke F, tako da je AC=AF. Sa slike se vidi da je 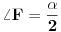 , odakle slijedi da su trouglovi BCF i ABD slicni ( 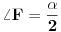 , ugao  je zajednicki). Prema tome, mozemo napisati sljedecu proporciju:
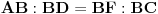 *
Posto je 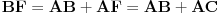 (jer je trougao ACF jednakokraki, pa je AF=AC) **
Jos imamo da je 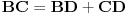 ***
Kad ** i *** zamjenimo u * dobijemo
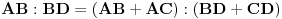
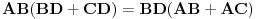
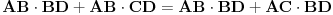
Nakon kracenja 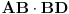 dobijemo
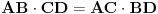
I na kraju
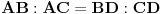
[att_img] [ Kolins Balaban @ 18.06.2007. 16:20 ] @
Vidim da sam zaboravio odgovoriti na dio pitanja. Tacan naziv teoreme ne znam, niti sam ga gdje pronasao. Teorema doslovno ovako glasi
Simetrala unutrasnjeg ugla trougla dijeli suprotnu stranicu iznutra na dijelove koji se odnose kao strane uz taj trougao.
Postoji jos jedna teorema, koja, moze se reci, ide uz ovu:
Simetrala vanjskog ugla trougla, dijeli naspramnu stranicu priduzenog mu unutrasnjeg ugla izvana na dijelove koji se odnose kao stranice unutrasnjeg njemu susjednog ugla trougla.
[ Farenhajt @ 18.06.2007. 16:48 ] @
Mislim da teorema i nema drugo ime. I po stranim izvorima najčešće se označava kao "Teorema o simetrali ugla (u trouglu)"
[ EArthquake @ 18.06.2007. 17:06 ] @
Citat: zivota11: hvala momci na pomoci, RMAN, jel upisujes E2 na FTN?
[Ovu poruku je menjao zivota11 dana 18.06.2007. u 14:00 GMT+1]
ok , za sad nas je trojica :) [ Daniel011 @ 18.06.2007. 17:12 ] @
Jednostavnije je preko sinusne teoreme:
[att_img]
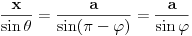
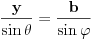
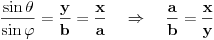 [ Farenhajt @ 18.06.2007. 17:25 ] @
Jeste brže preko sinusne, ali taj dokaz ne možeš izvesti đacima VII ili VIII razreda, a njima ova teorema za teže i takmičarske zadatke dobro dođe.
[ RMAN @ 18.06.2007. 17:59 ] @
@zivota11
Da upisujem E2 na FTN-u  [ Kolins Balaban @ 18.06.2007. 18:32 ] @
Upravo tako Farenhajt, ta teorema se spominje u osnovnoj skoli, obicno na dodatnoj nastavi, onda i u prvom razredu srednje skole, a posebno u drugom razredu, kad se radi homotetija, slicnost, Talesova teorema.... a to je sve prije trigonometrije. Tako je npr. Pitagorinu T. najlakse dokazati preko trigonometrije ili slicnosti, a to je nemoguce u VII razredu, pa se cesto dokaz i izostavlja na redovnoj nastavi.
PS: RMAN i EArthquake, sretno na prijemnom, pretpostavljam da je uskoro. Ako imate jos kakvih nedoumica, i mislite da mozemo jos pomoci, slobodno pitajte. Nemojte, da vam se desi, da vam dodje zadatak, a niste ga znali kod kuce, ili ste zapeli na nekoj maloj sitnici, za koju ste mislili da je nebitna, a zapravo je kljucna za rjesavanje zadatka, pa ste to i preskocili. Pozz
[ zivota11 @ 18.06.2007. 19:57 ] @
A meni nista srecno???
[ EArthquake @ 18.06.2007. 20:30 ] @
hehe hvala Kolins Balaban
jos 10 dana do prijemnog :)
[ Daniel011 @ 18.06.2007. 21:19 ] @
Citat: Kolins Balaban: Upravo tako Farenhajt, ta teorema se spominje u osnovnoj skoli, obicno na dodatnoj nastavi, onda i u prvom razredu srednje skole, a posebno u drugom razredu, kad se radi homotetija, slicnost, Talesova teorema....
Auu, da l' je moguće da je moja generacija toliko osakaćena za to znanje... Nama je nisu spomenuli ni jedan jedini put u toku celog školovanja, tako da je sad prvi put čujem. 
Zato bar imam ovaj 4um...  [ EArthquake @ 18.06.2007. 22:29 ] @
ako ti je za utehu , nisu je ni meni spominjali , kolko se ja secam bar :)
procitao sam je skorije , kad sam radio zadatak , u nekoj knjizi ili tkao nesto ...
[ Kolins Balaban @ 19.06.2007. 02:22 ] @
Sorry zovota11, sto sam tebe zaboravio. Srecno i tebi naravno, i svim onim koji izlaze na prijemni, bili posjetioci ovog foruma (podforuma) ili ne ;) Valjda ces mi oprostiti nekad :P
[ RMAN @ 19.06.2007. 08:49 ] @
Takodje hvala Kolins Balaban.
Bice gusto al cemo pokusati nesto da uradimo  [ zivota11 @ 19.06.2007. 14:33 ] @
Sve ti je oprosteno!!!
[ Kolins Balaban @ 19.06.2007. 15:37 ] @
Ehhh sad mogu lakse da disem :) puno ti hvala hehehehe
[ ivanujcic @ 20.06.2007. 07:55 ] @
Imamo dve formula za R i r (gore navedeno). Iz formule za R dobijamo da je 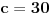 . Onda, iz formule za r i zamenom c dobijamo da 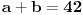 Kada kvadriramo dobijamo 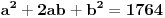 . Posto je
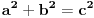 dobijamo da je 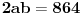 odnosno

Imamo dve jednacine koje resavamo kao sistem
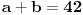

Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|