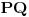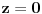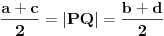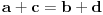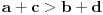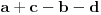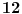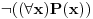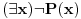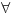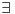|
|
[ Fitopatolog @ 21.09.2008. 11:27 ] @
|
| Običan sto sa četiri noge (može se smatrati da vrhovi nogu pripadaju jednoj ravni) se nalazi u kafiću čiji pod nije idealno ravan pa se zbog toga sto gega, t.j. oslanja se na pod samo sa tri noge dok četvrta "visi" u vazduhu. Da li se sto isključivo okretanjem oko svoje vertikalne ose može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u kom delu kafića se nalazi?
Dodatno potanje je da li se isto može postići ako vrhovi nogu stola ne pripadaju jednoj istoj ravni? |
[ Bojan Basic @ 21.09.2008. 13:51 ] @
Citat: Fitopatolog:
Da li se sto isključivo okretanjem oko svoje vertikalne ose može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u kom delu kafića se nalazi?
Ne.
Neka je pod takav da postoji kanal koji ide duž četvrtine kružnice koja prolazi kroz sve četiri noge. Stočić se „gega“ zato što je jedna noga u tom kanalu; jasno, kako god da ga okrenemo oko svoje vertikalne ose, uvek će tačno jedna noga biti u tom kanalu, i prema tome stočić će se uvek „gegati“.
Odgovor na dodatno pitanje takođe je negativan, sa sličnim obrazloženjem. [ Fitopatolog @ 21.09.2008. 17:18 ] @
Zanimljiv je granični slučaj, kada je jedna noga tačno na početku luka a druga tačno na kraju luka. Treba uzeti u obzir i širinu noge pri vrhu.
[ Daniel011 @ 21.09.2008. 18:47 ] @
Ako je potrebno obuhvatiti i taj granični slučaj, mogli bismo pretpostaviti da je taj kanal koji je Bojan opisao duži od četvrtine, a kraći od polovine kružnice i da mu se dubina linearno povećava od jednog njegovog kraja prema drugom. U jednom trenutku u tom kanalu može biti ili jedna noga, ili dve noge, ali ni u kom slučaju neće sve 4 noge dodirivati pod.
[ Bojan Basic @ 21.09.2008. 19:43 ] @
Citat: Fitopatolog:
Treba uzeti u obzir i širinu noge pri vrhu.
Da, posmatrao sam najprostiji model (kada su noge predstavljene tačkama). Danielova korekcija prolazi bez problema. [ Fitopatolog @ 23.09.2008. 19:28 ] @
Ako pretpostavimo da podovi u našim kafićima nemaju udubljenja i ispupčenja sa vertikalnim i veoma strmim stranama već su strmine vrlo blage (što je razumna pretpostavka za većinu naših kafića), tada se naš prethodni slučaj unekoliko menja. Da li u takvoj situaciji možemo naći položaj stola u kome se on ne gega?
[ Bojan Basic @ 25.09.2008. 04:47 ] @
Pre svega, primetio sam popriličnu rupu u postavci. Naime, rotacija ti nije dobro definisana: kažeš da rotiramo sto oko njegove ose, a tu osu ne možeš odrediti ako sto ne stoji sa sve četiri noge na zemlji (jer se sto onda „gega“, i postavlja se pitanje koji od tih položaja odabrati kao merodavan za određivanje ose). Ipak, pošto u istoj rečenici u kojoj objašnjavaš rotiranje osu nazivaš vertikalnom (iako je ona vertikalna samo u vrlo specijalnom slučaju, kada je ravan stola horizontalna), pretpostavljam da si se samo nespretno izrazio, i da zapravo želiš rotaciju oko vertikalne prave koja prolazi kroz centar kvadrata određenog podnožjima nogu. Ostatak poruke napisan je podrazumevajući ovo tumačenje, a ti ćeš me već ispraviti ako si mislio na nešto drugo.
Citat: Fitopatolog:
Ako pretpostavimo da podovi u našim kafićima nemaju udubljenja i ispupčenja sa vertikalnim i veoma strmim stranama već su strmine vrlo blage (što je razumna pretpostavka za većinu naših kafića), tada se naš prethodni slučaj unekoliko menja. Da li u takvoj situaciji možemo naći položaj stola u kome se on ne gega?
Drugim rečima, pooštravaš uslove tako što zahtevaš da funkcija koja oslikava udubljenje bude neprekidna. U tom slučaju možemo rotacijom za pogodan ugao postići da se sto ne „gega“.
Pre svega, treba ustanoviti uslov koji garantuje da se sve četiri noge oslanjaju na pod (u zavisnosti, naravno, od dubina/visina poda pod nogama — označimo ih sa  ,  ,  i  , ciklično). Pretpostavimo da sto stoji stabilno. Podnožja sve četiri noge nalaze se u temenima jednog kvadrata, čiji ćemo centar obeležiti sa  . Obeležimo još sa  tačku koja ima  i  koordinate iste kao i tačka  , i  koordinatu jednaku  . Posmatrajmo sada vertikalnu ravan određenu tačkama u kojima dve međusobno naspramne noge dodiruju pod. Duž 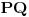 možemo posmatrati kao srednju liniju jednog pravouglog trapeza u toj ravni: njegove osnovice protežu se od dodirnih tačaka nogu i poda do ravni 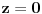 . U zavisnosti od toga koji smo par naspramnih nogu posmatrali, dobijamo 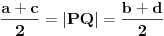 , te je potreban uslov da sve četiri noge dodiruju pod upravo 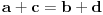 . Ovaj uslov je i dovoljan, jer je ravan jednoznačno određena trima nekolinearnim tačkama, te uvek možemo proizvoljno odabrati tri vrednosti i četvrta je odmah određena.
Dakle, ako u početnom momentu sto nije stabilan, možemo pretpostaviti, bez umanjenja opštosti, da važi 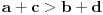 . Rotirajmo sto za četvrtinu kruga; veličine  ,  sada su zamenile vrednosti s veličinama  ,  , međusobno, te se znak u navedenoj nejednakosti okrenuo. Međutim, zbog neprekidnosti funkcije koja oslikava udubljenje, i funkcija 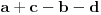 (u zavisnosti od ugla rotacije) takođe je neprekidna. Kako je u polaznom momentu njena vrednost pozitivna, a u krajnjem negativna, prema teoremi o srednjoj vrednosti ova funkcija ima nulu, tj. bar u jednom momentu važi jednakost 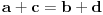 , i tada je sto stabilan. Ovim je dokaz završen.
Citat: Fitopatolog:
Dodatno potanje je da li se isto može postići ako vrhovi nogu stola ne pripadaju jednoj istoj ravni?
Odgovor na ovo pitanje nešto je jednostavniji: ne može, što pokazuje primer potpuno ravnog poda. 
[ galet@world @ 30.09.2008. 15:17 ] @
Citat: Bojan Basic:
Odgovor na ovo pitanje nešto je jednostavniji: ne može, što pokazuje primer potpuno ravnog poda. :)
Ovo nije tačno! Primer ravnog poda to ne pokazuje.
Primer ravnog poda važi samo za ravan pod, a sto sa četiri nejednake noge može da stoji na sve četiri noge
ako je pod takva kriva površina da dodiruje sve noge.
A u zadatku lepo stoji da pod u kafiću nije idealno ravan. [ Bojan Basic @ 30.09.2008. 15:39 ] @
Citat: galet@world:
a sto sa četiri nejednake noge može da stoji na sve četiri noge
ako je pod takva kriva površina da dodiruje sve noge.
Ne samo što su noge nejednake, već njihovi vrhovi ne pripadaju istoj ravni (u tom obliku je Fitopatolog naveo uslov). Dakle, nikako se ne može postići da se sve četiri noge stola oslanjaju na ravan pod, jer bi to značilo da im vrhovi pripadaju istoj ravni.
Citat: galet@world:
A u zadatku lepo stoji da pod u kafiću nije idealno ravan.
Dobro, u tom slučaju pretpostavi da je ravno samo parče poda kod našeg stola, a da je ostatak kriv (što nam uopšte ne smeta, jer sto vrtimo na jednom te istom mestu). Je li sad u redu? [ Daniel011 @ 30.09.2008. 15:56 ] @
Citat: galet@world: A u zadatku lepo stoji da pod u kafiću nije idealno ravan.
Ali to ne smeta da se prihvati Bojanovo obrazloženje. Pitanje je, u tom delu, bilo vrlo precizno:
Citat: Fitopatolog: Da li se sto isključivo okretanjem oko svoje vertikalne ose može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u kom delu kafića se nalazi?
Znači, neka se sto, kome su noge nejednake, nalazi u takvom delu kafića na kome je ravan onaj deo poda po kome se kreću noge pri rotaciji stola, a van i unutar tog dela, tj. te kružnice, mogu se nalaziti i udubljenja i ispupčenja. Samim tim je zadovoljen uslov da pod nije ravan. A pošto je dozvoljena isključivo rotacija, a ne i translacija stola, od interesa je samo ta kružnica. Prema tome, odgovor za taj slučaj jeste NE.
Zapravo, sad vidim, rekao sam isto što i Bojan, samo drugim rečima. [ Fitopatolog @ 30.09.2008. 20:03 ] @
Zaključak: ako se nađete u situaciji da se sto za kojim sedite gega, setite se Bojanovog objašnjenja: Rotirajte sto dogod se ne uravnoteži. Ako sto ipak ne može da se uravnoteži, znajte da mu noge nisu iste dužine.
P.S. Proveravao sam, ovo funkcioniše!
[ Daniel011 @ 30.09.2008. 20:17 ] @
S tim da, ako sto može da se uravnoteži, to ne mora da znači da su mu noge iste dužine.
Tj. implikacija važi samo u jednom smeru.  [ galet@world @ 30.09.2008. 21:19 ] @
Citat: Bojan Basic: Dobro, u tom slučaju pretpostavi da je ravno samo parče poda kod našeg stola, a da je ostatak kriv (što nam uopšte ne smeta, jer sto vrtimo na jednom te istom mestu). Je li sad u redu?
Nije.
Na pitanje: " da li se isto može postići ako vrhovi nogu stola ne pripadaju jednoj istoj ravni?"
Odgovorio si: "ne može........"
Eto taj odgovor nije tačan.
Tačkice u tvom odgovoru odnose se na objašnjenje da to nije moguće postići na ravnom podu,
što je suvišno, jer svi znamo da su vrhovi tri bilo koje noge u nekoj ravni a četvrti nije.
Tačan odgovor je - To se može postići uz uslov da četvrta noga nije prekratka pa se u kafiću
ne može nigde naći zadovoljavajuće mesto, međutim, ako to nije slučaj onda ne možeš tvrditi
da za neku dužinu kraće noge u kafiću ne postoji zadovoljavajuće mesto.
Ako sto postaviš na to mesto on se neće gegati, ali ako ga na tom istom mestu zarotiraš za
neki ugao oko vertikalne osovine i pustiš ga videćeš da jedna noga "visi", a ako ga vratiš za isti
ugao - neće visiti ni jedna noga.
Uostalom - može i ovako: Stavi sto sa jednakim nogama na bilo koje mesto u kafiću, on će da
se klacka ili gega na one dve noge koje uvek dodiruju pod, a sad jednu od te dve noge skrati
tačno toliko da sve četiri noge na tom mestu dodiruju pod.
I sad imaš sto sa jednom nogom kraćom i mesto gde se on u određenom položaju ne gega.
[ Bojan Basic @ 30.09.2008. 22:27 ] @
Ne razumeš šta se u matematici podrazumeva pod dokazivanjem a šta pod opovrgavanjem nekog stava. Ako nešto dokazujemo, obrazložićemo zašto je dotična tvrdnja uvek istinita; ako pak nešto opovrgavamo, dovoljno je naći jedan primer koji ilustruje suprotno.
U ovom slučaju imamo stav koji kaže da se sto čiji vrhovi nogu ne pripadaju istoj ravni može opisanom rotacijom dovesti u stabilan položaj. Taj stav sam opovrgao tako što sam dao primer koji ilustruje suprotno.
[ zzzz @ 30.09.2008. 23:10 ] @
Ma jasno je meni da sto koji ima tri noge od 70 cm a četvrtu od 45 cm nećemo
moći lako uravnotežiti na razumno grbavom podu kafića.Ali neka su noge idealno jednake.A pod grbav tako da ni u jednom slučaju ne postoje četiri pogodne tačke
za uravnoteživanje tog idealnog stola.Rotiraj, vuci, naginji ...
Moje iskustvo je da samo čep od piva rješava taj problem, a vi kako hoćete.
[ galet@world @ 01.10.2008. 18:40 ] @
Tako je Milane! Još bi bilo zgodnije kad bi od kuće poneo klin jer čep ponekad ne odgovara.
Klin možeš u principu da uguraš tačno koliko treba čak i pod kraću nogu.
A koliko treba?
Ako nedovoljno uguraš klin sto će i dalje da se klati oslanjajući se na dve dijagonalne noge,
a ako kliin uguraš previše opet će sto da se klati, ali oslanjajući se na druge dve dijagonalne
noge.
Odavde sledi da se klin može ugurati tačno toliko da nema klaćenja ni oko jedne dijagonale.
Klin možemo smatrati sastavnim delom poda ili klin ne moramo ni da upotrebimo ako nađemo mesto
gde je pod ispod kraće noge baš toliko uzdignut.
Kako naći to mesto?
Sad ću ja da pokušam da opovrgnem „opovrgavanje“
Neka su tri jednake noge dužine l, a četvrta neka je kraća za ∆l
Vrhovi tri jednake noge određuju ravan (x,y) koja preseca zakrivljenu površinu poda. Vrh
kraće noge je, naravno, udaljen od te ravni za dužinu ∆l .
Ako kroz vrh četvrte (kraće) noge postavimo normalu na ravan određenu vrhovima jednakih nogu, onda će ta
normala probosti i tu ravan i krivu površinu poda. Označimo udaljenost između ta dva probodišta sa ∆z.
Promatrajmo situaciju kada se probodište kroz površinu poda nalazi između vrha kraće noge
i probodišta kroz ravan koju određuju vrhovi tri jednake noge t. j. pod je ispupčen prema
kraćoj nozi.
Ako je kriva površina poda takva da je ∆z promenljivo i zavisno od mesta gde se sto nalazi,
t. j. ∆z = f(x,y) i od orijentacije stola, i ako je ∆zmax < ∆l onda se na takvoj površini sto ne
može stabilizovati, međutim, ako je kontinualna površina poda takva da je ∆zmin < ∆l < ∆zmax t. j. ∆z
poprima i veće i manje vrednosi od ∆l onda na nekom mestu mora imati i vrednost jednaku ∆l. Na
takvom mestu sto stoji stabilno na sve četiri noge.
Time je opovrgnuta tvrdnja da se sto sa jednom kraćom nogom ne može stabilizovati ni na jednom neravnom podu.
[ Daniel011 @ 01.10.2008. 20:05 ] @
Citat: galet@world: Time je opovrgnuta tvrdnja da se sto sa jednom kraćom nogom ne može stabilizovati ni na jednom neravnom podu.
To niko nije tvrdio.
Zašto lepo ne pročitaš kako je glasilo pitanje?
Citiraću ga još ovaj (i poslednji) put:
Citat: Da li se sto isključivo okretanjem oko svoje vertikalne ose može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u kom delu kafića se nalazi?
Dodatno potanje je da li se isto može postići ako vrhovi nogu stola ne pripadaju jednoj istoj ravni?
Drugim rečima se ovo pitanje može iskazati: Da li se uvek, bez obzira na oblik zakrivljenja poda, sto koji ima nejednake dužine nogu, rotacijom oko svoje ose, može dovesti u položaj u kome se neće klatiti?
Odgovor na ovo pitanje je NE, što je i dokazano kontraprimerom.
Ti očigledno pitanje tumačiš na drugi način, a tvoja interpretacija tog pitanja bi glasila: Da li postoji takav oblik zakrivljenja poda, pri kome se sto koji ima nejednake dužine nogu, rotacijom oko svoje ose, može dovesti u položaj u kome se neće klatiti?
Odgovor na ovo pitanje je DA, što si i sam objasnio. Ali, to nije ono pitanje koje je postavio autor teme.
[ Bojan Basic @ 01.10.2008. 20:15 ] @
Galet@world, vidi ovako. Fitopatolog je postavio, zamislimo, pitanje da li u trouglu uvek postoji prav ugao. Na to ja odgovoram: „Ne, što pokazuje primer jednakostraničnog trougla“. Slažeš li se, za početak, da ovo jeste ispravan odgovor na takvo pitanje? Zatim se javljaš ti i tvrdiš da ja nisam u pravu, rečima: „Ako uzmemo trougao čije su stranice  ,  i  , onda jedan njegov ugao jeste prav“.
Razumeš li sada zašto to što ti pričaš, iako jeste tačno, nije odgovor na Fitopatologovo pitanje? [ galet@world @ 02.10.2008. 11:25 ] @
Ovako glasi zadatak:
"Običan sto sa četiri noge (može se smatrati da vrhovi nogu pripadaju jednoj ravni) se nalazi u kafiću čiji pod nije idealno ravan pa se zbog toga sto gega, t.j. oslanja se na pod samo sa tri noge dok četvrta "visi" u vazduhu. Da li se sto isključivo okretanjem oko svoje vertikalne ose može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u kom delu kafića se nalazi?
Dodatno potanje je da li se isto može postići ako vrhovi nogu stola ne pripadaju jednoj istoj ravni?"
Dozvolite da preciziram to dodatno pitanje:
Da li se sto isključivo okretanjem oko svoje vertikalne ose može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u kom delu kafića se nalazi ako vrhovi nogu stola ne pripadaju istoj ravni?
Decu u školi uče da na pitanje odgovaraju tako što će deo pitanja ponoviti.
Na primer na pitanje "Koliko godina ima meseci" treba odgovoriti "Godina ima dvanaest meseci", a ne samo "Dvanaest"
Na pitanje koje se odnosi na sto sa jednakim nogama Bojan odgovara:
"U tom slučaju možemo rotacijom za pogodan ugao postići da se sto ne „gega“."
Poštujući navedeno načelo odgovor bi trebalo, na primer, da ovako glasi:
Sto sa četiri noge u istoj ravni može se isključivo okretanjem oko svoje vertikalne ose dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u kom delu kafića se nalazi.
Na dodatno pitanje Bojan odgovara ovako:
"ne može, što pokazuje primer potpuno ravnog poda."
a "školski" odgovor trebalo bi da glasi ovako ili slično:
"Ako vrhovi nogu stola ne pripadaju istoj ravni onda se sto isključivim okretanjem oko svoje vertikalne ose ne može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u kom delu kafića se nalazi, što pokazuje primer potpuno ravnog poda."
Ovakav odgovor na dodatno pitanje, naravno, nije tačan - stoga je Bojan u svom odgovoru trebalo da bude ili jasniji ili precizniji.
Ti Daniele011 ubacuješ reč "uvek" iako ona u zadatku nigde ne postoji. Nesporazum je u tumačenju reči "bez obzira" jer se mogu dvojako protumačiti.
Na primer u prvom "školskom" odgovoru reči "bez obzira" znače da ne treba voditi računa o tome gde se sto nalazi - sto se uvek može stabilizovati bilo gde da se nalazi.
Ako se u drugom "školskom" odgovoru reči "bez obzira" tako shvate onda odgovor nije tačan jer može da postoji mesto gde sto stoji stabilno na sve četiri noge.
Reči "bez obzira" u drugom odgovoru mogu se shvatiti i drukčije. One mogu da znače da ne smemo u tom slučaju postupati "bez obzira" već moramo uzeti u obzir konfiguraciju poda
ili će bit jasnije ako kažemo - sto ne možemo dovesti u stabilno stanje "bez obzira" gde se nalazi već to moramo uzeti u obzir kod "ćopavog" stola.
Prema tome treba davati jasne i nedvosmislene odgovore bez mogućnosti drukčijeg tumačenja.
Uostalom, ako mislite da nisam u pravu onda precizno formulišite samostalne (školske) odgovore na oba pitanja, jer je očigledno da smo o samom problemu "geganja" stola potpuno saglasni
ali nismo saglasni oko tumačenja zahteva zadatka ni u formulaciji odgovora.
[ Daniel011 @ 02.10.2008. 12:16 ] @
Pošto insistiraš na školskim odgovorima, kako bi, po tebi, trebalo da glasi odgovor na Bojanovo pitanje (uz malo izmenjene reči, ali isti smisao): "Da li u trouglu postoji prav ugao, bez obzira na dužine njegovih stranica?" Na to pitanje ćeš dobiti odgovor NE. Ali ti onda kažeš, taj odgovor nije školski, školski odgovor treba da glasi: "U trouglu ne postoji prav ugao, bez obzira na dužine njegovih stranica." I zatim dodaš - "takav odgovor je, naravno, pogrešan" - što i jeste, jer mu je izmenjen smisao u odnosu na onaj prvobitni odgovor NE. Ako se već daje školski odgovor, ne može se deo pitanja ponoviti baš od reči do reči.
Uostalom, i sam si primetio da izraz "bez obzira" ne znači isto u pitanju i u odgovoru. Samim tim ne možeš ni insistirati na tome da se "bez obzira" jednostavno prepiše i u odgovor.
Ja bih školski odgovor na to pitanje formulisao ovako: "U trouglu ne postoji uvek prav ugao; da li će postojati prav ugao, zavisi od dužina njegovih stranica."
Već si primetio da sam izraz "bez obzira" zamenio izrazom "uvek". U ovom kontekstu smatram to pogodnom interpretacijom.
Školski odgovor na pitanje u vezi stola bi, samim tim, mogao da glasi "Sto čiji vrhovi nogu ne pripadaju jednoj ravni, ne može se uvek, rotacijom oko svoje vertikalne ose, dovesti u položaj u kome će se sve četiri noge oslanjati na neravni pod."
Ako ti smeta reč "uvek", slobodno je zameni izrazom "pri bilo kom obliku neravnine poda", neće se mnogo izmeniti smisao.
Mada, ako je pitanje nedvosmisleno i precizno (a jeste), dovoljno je na njega odgovoriti samo sa DA ili NE (što je već i učinjeno) i ne vidim koja je svrha insistiranja na školskim odgovorima.
[ galet@world @ 02.10.2008. 18:07 ] @
Citat: Daniel011: i ne vidim koja je svrha insistiranja na školskim odgovorima.
Ako ne vidiš - progledaj!
Odgovor je u principu tvrdnja. Tvrdnja mora da sadrži i zagonetku i nedvosmislen odgovor na zagonetku. [ Bojan Basic @ 02.10.2008. 21:23 ] @
Citat: galet@world:
Tvrdnja mora da sadrži i zagonetku i nedvosmislen odgovor na zagonetku.
To si mogao čuti od učiteljice, a čak je i kod nje pitanje koliko je na takvim stvarima insistirala tokom časa matematike. Ipak, matematika je malo odmakla od prva četiri razreda osnovne škole. U bilo kojoj zbirci iznad tog nivoa odgovor na pitanje „Koliko godina ima meseci?“ glasio bi: „Odgovor je 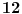 . Zaista, ... [ovde sledi dokaz]“; uzmi bilo koji ozbiljniji matematički tekst, i pokušaj da jednu stranicu (po sopstvenom izboru) „prevedeš“ na jezik za koji se zalažeš. Od te jedne dobio bi tri ili četiri stranice, pri čemu čitaocu ne bi saopštio ama baš ni jednu jedinu novu informaciju. Normalno, svaki matematičar će se potruditi da što konciznije izloži ono što želi (dokle god to nije na uštrb jasnoće), a ne da na silu razvlači svoj tekst tako da zauzme tri ili četiri puta više stranica nego što je realno. E sad, od svih učesnika na ovoj temi jedino ti nisi shvatio moje reči (ako zaista nisi shvatio, tj. ako se ne pretvaraš), te bih konstatovao da moje izražavanje nije išlo na uštrb jasnoće, i da se, prema tome, sasvim uklapa u ovo o čemu sam pisao u tekućem pasusu.
Nego, pitao bih te nešto. Zašto očekuješ da mi odgovaramo na tvoje stavove, a da ti uporno ignorišeš naša pitanja. Nešto sam pitao, Daniel je to ponovio, a ti si sve elegantno izignorisao i nastavio sa svojom pričom. Ako bi želeo da nastaviš razgovor, bilo bi lepo da nas udostojiš odgovora na pitanje koje ću još jednom ponoviti:
Citat: Daniel011:
Pošto insistiraš na školskim odgovorima, kako bi, po tebi, trebalo da glasi odgovor na Bojanovo pitanje (uz malo izmenjene reči, ali isti smisao): "Da li u trouglu postoji prav ugao, bez obzira na dužine njegovih stranica?"
Ako pak ne umeš tako odgovoriti na ovo pitanje da odgovor ne izazove smeh kada se uporedi s jednostavnim, potpuno jasnim i, nadasve, tačnim odgovorom „Ne“ (uz navođenje primera jednakostraničnog trougla, recimo), onda možemo polako i završavati ovo. [ miki069 @ 02.10.2008. 22:26 ] @
Galet@world u pravu su Bojan i Danijel.
"bez obzira" ima tezinu univerzalnog kvantifikatora (za svako) a ne egzistencijalnog (postoji).
Koji je odgovor na pitanje: "da li su tacke udaljene 10cm od preseka dijagonala poda kafica, bez obzira gde se te tacke nalaze na podu kafica?"
Odgovor je: NE
jer ovom konstrukcijom "bez obzira gde se nalaze" isto je kao da sam rekao "sve tacke"
[ galet@world @ 03.10.2008. 10:47 ] @
Citat: Bojan Basic: Ako pak ne umeš tako odgovoriti na ovo pitanje da odgovor ne izazove smeh kada se uporedi s jednostavnim, potpuno jasnim i, nadasve, tačnim odgovorom „Ne“ (uz navođenje primera jednakostraničnog trougla, recimo), onda možemo polako i završavati ovo.
Već sam rekao da se reči "bez obzira" mogu dvojako razumeti što ni ti nisi osporio.
Zato je Daniel011 to i uvažio i odgovorio na tvoje pitanje bez upotrebe tih reči.
A zašto ti insistiraš na tome da ja odgovorim u stilu proročanstava u Delfima pa
posle moj odgovor možeš tumačiti kako ti je drago ili kazati da je neodređen ili - kao
što si rekao - da te uveseljava?
I ja sam od tebe tražio da daš kompletan i samostalan odgovor na
dodatno pitanje bez pozivanja na to pitanje čak i bez pominjanja tog pitanja, koji
se može razumeti sam za sebe kao tvrdnja i biti nedvosmislen pa to ipak nisi učinio.
Ne mora biti "školski" ali ne sme biti ni dvoznačan.
Nadam se da nećeš da kažeš da je to nemoguće!
[ Bojan Basic @ 05.10.2008. 22:50 ] @
Citat: galet@world:
Već sam rekao da se reči "bez obzira" mogu dvojako razumeti što ni ti nisi osporio.
Ako tvrdiš da nisam osporio, evo sad osporavam.
Citat: galet@world:
A zašto ti insistiraš na tome da ja odgovorim u stilu proročanstava u Delfima
Ne, insistiram na upravo suprotnom: da napišeš odgovor onako kako bi on, po tvom mišljenju, morao da izgleda. Tvrdiš da je jedno obično „Ne“ nezadovoljavajuće — e pa onda pokaži kako bi trebalo.
Citat: galet@world:
I ja sam od tebe tražio da daš kompletan i samostalan odgovor na
dodatno pitanje bez pozivanja na to pitanje čak i bez pominjanja tog pitanja, koji
se može razumeti sam za sebe kao tvrdnja i biti nedvosmislen pa to ipak nisi učinio.
Ne mora biti "školski" ali ne sme biti ni dvoznačan.
Nadam se da nećeš da kažeš da je to nemoguće!
Nisam primetio da si to tražio, ali svejedno to činim sada.
Pitanje: Da li u trouglu postoji prav ugao, bez obzira na dužine njegovih stranica?
Moj odgovor: Ne, što pokazuje primer jednakostraničnog trougla.
Odgovor na kakvom ti insistiraš: U trouglu ne postoji uvek prav ugao, što pokazuje primer jednakostraničnog trougla.
Ovde bih istakao nekoliko „sitnica“:
1. Fraza bez obzira očigledno ne nosi sa sobom dvosmislenost pitanja (ako tvrdiš suprotno, navedi dva različita tumačenja gornjeg pitanja).
2. Prvonavedeni odgovor savršeno je jasan (ako tvrdiš suprotno, navedi šta je ostalo nejasno posle tog odgovora).
3. Odgovor na kakvom ti insistiraš znači potpuno isto što i onaj iznad, ali je za njega potrošeno mnogo više reči (ovde nemaš s čim da se ne složiš, prosto izbroj reči).
4. Fraza bez obzira iz postavke u odgovoru na kakvom ti insistiraš može se i mora zameniti frazom uvek. Zaista, zamena je očigledno moguća budući da drugonavedeni odgovor jeste odgovor na postavljeno pitanje; s druge strane, zamena je i obavezna, jer odgovor „U trouglu ne postoji prav ugao, bez obzira na dužine njegovih stranica, što pokazuje primer jednakostraničnog trougla“ očito nije tačan (opet, ako se s nečim ne slažeš, lepo napiši gde sam pogrešio i kako po tvom mišljenju treba da bude).
Posebno je bitno uporediti prvu i četvrtu stavku: fraza bez obzira u pitanju nije ni najmanje dvosmislena, ali u odgovoru je ne valja koristiti.
Evo ti još bolje ilustracije. Ako te ja pitam „Jesi li nekad bio na Mesecu?“ i ti odgovoriš „Ne“, to je savršeno jasno, bez trunke dvosmislenosti; s druge strane, ako bi hteo da proširiš odgovor tako da bude samostalan, on bi morao glasiti „ Nikad nisam bio na Mesecu“, a ne bi glasio „Nekad nisam bio na Mesecu“. Poenta: „proširivanje“ odgovora ne radi se tako što prosto prepišeš pitanje i udeneš ne, već se određeni „kvantifikatori“ menjaju. Kad pokušamo da ovaj jezičku zavrzlamu matematički formalizujemo, dobijamo nešto ovakvo:
Pitanje: Da li  ?
Moj odgovor: 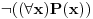 (dakle, za celo gornje tvrđenje stavljam jedno „ne“).
Odgovor na kakvom ti insistiraš: 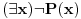 (ovde se ne možeš pozvati na tvrđenje „u paketu“, već moraš celu rečenicu formulisati ispočetka, i primeti da je pri tom 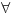 prešlo u prešlo u 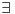 ).
Uzimajući sve u obzir, gornji „blok“ na primeru polaznog pitanja izgleda ovako:
Pitanje: Da li se sto isključivo okretanjem oko vertikalne prave koja prolazi kroz centar kvadrata određenog podnožjima nogu može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod, bez obzira u kom delu kafića se nalazi?
Moj odgovor: Ne, što pokazuje primer ravnog poda.
Odgovor na kakvom ti insistiraš: Sto se isključivo okretanjem oko vertikalne prave koja prolazi kroz centar kvadrata određenog podnožjima nogu ne može uvek dovesti u stanje da se sa sve četiri noge oslanja na neravni pod, što pokazuje primer ravnog poda.
E, ovo poslednje je ono za šta sam u prethodnoj poruci rekao da izaziva smeh. Ako tebi to nije smešno već si uveren da je baš tako jedino ispravno, ja tu stvarno ništa ne mogu, živi u kakvom uverenju hoćeš. [ Daniel011 @ 06.10.2008. 16:33 ] @
E, a sad će Galet garant reći da je na njegovo pitanje
Citat: galet@world: A zašto ti insistiraš na tome da ja odgovorim u stilu proročanstava u Delfima pa
posle moj odgovor možeš tumačiti kako ti je drago ili kazati da je neodređen ili - kao
što si rekao - da te uveseljava?
trebalo da daš "školski", "samostalan" i "nedvosmislen" odgovor koji počinje ovako:
"Ja insistiram na tome da ti odgovoriš u stilu proročanstava u Delfima pa da posle tvoj odgovor mogu tumačiti kako mi je drago ili kazati da je neodređen ili - kao što sam rekao - da me uveseljava, zbog toga što... (itd.)"  [ galet@world @ 08.10.2008. 11:05 ] @
. Možda moji odgovori zvuče svađalački, ali ja svađu zaista ne želim. Ja samo želim razumevanje.
Citat: Bojan Basic:Tvrdiš da je jedno obično „Ne“ nezadovoljavajuće — e pa onda pokaži kako bi trebalo
ovako:
Utrouglu ne postoji prav ugao bez obzira na dužine njegovih stranica već on postoji s obzirom na dužine njegovih stranica.
Podvučene reči sam dodao zato da se prethodne reči ne mogu tumačiti na proizvoljan način. Pod obzirom se, naravno, podrazumeva
Pitagorina teorema.
Citat: Nisam primetio da si to tražio, ali svejedno to činim sada.
Tražio sam u poruci od 10. 2. - poslednja dva reda
Citat: 1. Fraza bez obzira očigledno ne nosi sa sobom dvosmislenost pitanja (ako tvrdiš suprotno, navedi dva različita tumačenja gornjeg pitanja).
Navešću na kraju poruke.
Citat: 2. Prvonavedeni odgovor savršeno je jasan (ako tvrdiš suprotno, navedi šta je ostalo nejasno posle tog odgovora).
On je jasan, ali sam za sebe ne kaže na šta se odnosi.
Citat: 3. Odgovor na kakvom ti insistiraš znači potpuno isto što i onaj iznad, ali je za njega potrošeno mnogo više reči (ovde nemaš s čim da se ne složiš, prosto izbroj reči)
Izbrojao sam i ne slažem se zato što takvom odgovoru treba dodati reči sadržane u pitanju.Taj odgovor važi samo ako se ispred njega stavi pitanje.
Citat: 4. Fraza bez obzira iz postavke u odgovoru na kakvom ti insistiraš može se i mora zameniti frazom uvek.
Ne mora. Ja sam odgovorio na to pitanje bez te fraze.
Citat: „Nikad nisam bio na Mesecu“ . Tako je na srpskom jeziku, a kako je na drugim jezicima?
Citat: Pitanje: Da li se sto isključivo okretanjem oko vertikalne prave koja prolazi kroz centar kvadrata određenog podnožjima nogu može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod, bez obzira u kom delu kafića se nalazi?
Mislim da si prefomulisao pitanje jer ono bi po zadatku trebalo da glasi:
Da li se sto isključivo okretanjem oko svoje vertikalne ose može dovesti u stanje da se sa sve četiri noge oslanja na neravni pod bez obzira u
kom delu kafića se nalazi ako vrhovi nogu stola ne pripadaju istoj ravni?
Nigde se ne pominje kvadrat, ali to nije bitno.
Ti si ovde reči "bez obzira u kom delu kafića se nalazi" poistovetio sa "u svakom delu kafića", a ja sam te reči protumačio kao "u bilo kom delu kafića"
Zašto?
Zato što bi, ako se misli na svaki deo kafića, pitanje trebalo tako i da glasi. Osim toga i ti si započeo sa odgovaranjem na zadatak tretirajući jedan
određen deo kafića na kom postoji udubljenje u koje može da upadne samo jedna noga stola. Zar ne?
Prema tome tvoji odgovori su tačni ako se pitanje odnosi na svaki deo iliti sve delove kafića, ali i tu treba biti oprezan jer odgovor DA za sto sa jednakim nogama znači da se to može učiniti na
svakom mestu u kafiću, ali odgovor NE za ćopavi sto ili ćopavi sto se NE MOŽE stabilizovati na svakom mestu u kafiću, dvoznačan je jer se može protumačiti da takvo mesto uopšte ne postoji
t. j. da se odgovor odnosi na sva mesta, ali i da se ne odnosi na sva mesta nego samo na neka pa, prema tome, nisu sva mesta uključena.
Ako bi se pitanje odnosilo na "bilo koji deo kafića" onda je odgovor DA za svaki deo kafića za sto sa jednakim nogama, ali isto tako bi odgovor bio DA ili MOŽDA i za ćopavi sto jer
može da postoji mesto gde se taj sto može stabilizovati. Dakle, reči "bez obzira" ni u pitanju nisu jasne.
[Ovu poruku je menjao galet@world dana 09.10.2008. u 16:06 GMT+1][ galet@world @ 10.10.2008. 18:16 ] @
Citat: Bojan Basic:
U trouglu ne postoji uvek prav ugao, što pokazuje primer jednakostraničnog trougla.
Kako protumačiti izraze:
1. Ne postoji uvek
2. Uvek ne postoji
3. Nikad ne postoji
Da li je fraza "uvek" sa negacijom jednoznačno određena?
Da li je činjenicu da pravi ugao u trouglu nekad postoji a nekad ne moguće jednoznačno saopštiti uz upotrebu fraze uvek
Postoji li pravilo kog bi trebalo, u ovom smislu, da se pridržavaju predavači, odnosno autori udžbenika.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|