Teorija redova - Kosijev kriterijum

[ RMAN @ 17.10.2008. 20:01 ] @

Pozdrav!
Ima neke nedoumice sa jednim zadatkom pa ako moze mala pomoc

E ovako:
Ispitati da li je red

konvergira. Treba ispitati preko Kosijevog kriterijuma.

Kosijev kriterijum kaze:
Red

konvergira akko

postoji

vazi sledeca implikacija:

E sad:
Izraz

je sigurno manji ili jednak od

. Nadam se da nisam pogresio.
Iz ovoga je

a iz ovoga sledi da je

Sad me interesuje da li sam do sada napravio neku gresku i kako iz ovoga sto sam napisao da dokazem da niz divergira??

_{[Ovu poruku je menjao RMAN dana 17.10.2008. u 22:02 GMT+1]}

[ peddja_stankovic @ 17.10.2008. 23:00 ] @

za sada samo hint, ne valja ti ovaj kraj, ti hoces da dokazes da red konvergira a on ustvari divergira, treba da dokazes da vazi negacija kosijevog kriterijuma ...

[ RMAN @ 17.10.2008. 23:55 ] @

Znam da treba da dokazem negaciju, video sam u knjizi. Ali sta ako dobijem neki zeznutiji zadatak? kako onda da provalim kojim putem da idem?

[ h4su @ 18.10.2008. 00:59 ] @

Mozda grijesim al kad zakljucis da je suma reda manja od

nisi nista dobio s obzirom da to vazi za svako p iz N,tj taj izraz moze biti beskonacno (n=k+1 mozemo reci da je k fiksirano do k+p pri cemu je p iz N)

[ peddja_stankovic @ 18.10.2008. 07:45 ] @

Citat:

Znam da treba da dokazem negaciju, video sam u knjizi. Ali sta ako dobijem neki zeznutiji zadatak? kako onda da provalim kojim putem da idem?

Pitanje je previse hipoteticko. Na svim fakultetima se Kosijev kriterijum koristi u zadacima vise kao teorijsko pitanje a ne kao neki operativni kriterijum za dokazivanje konvergencije redova, ja sam video mozda tri zadatka na tu temu.

Inace, verovatno si video resenje u knjizi za postavljeno pitanje. Koristi se cinjenica da je 1/(k+1) + 1/(k+2) + ... + 1/(k+k) > 1/(2k) + 1/(2k) + ... + 1/(2k) = k*1/(2k) = 1/2 pa vazi negacija kosijevog kriterijuma

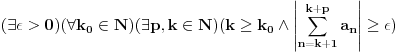
epsilon ti je 1/2 i p=k

[ Nedeljko @ 18.10.2008. 11:29 ] @

,

a to je svakako veće od, na primer,

, kakvo god da je