http://www.merriam-webster.com/dictionary/tangent
Tangenta NIJE bilo koja prava koja dodiruje neku krivu liniju u ravni.

Smerovi tangente i krive na mestu dodira su jednaki, ali to nije odgovor na postavljena pitanja.

Kreni sa jednostavnim primerom.

Jednačina kružnice sa poluprečnikom 1 i centrom u (0,0) je x^2+y^2=1
Tangenta na kružnicu u tački (0,1) je y=1.

Tačka (0,1) pripada i kružnici i tangenti. Ne postoji ni jedna druga tačka koje pripadaju i pravoj i tangenti.

Dekle, kada se priča o tangenti, smisao iskaza da se kriva i tangenta "dodiruju" je da imaju tačno 1 tačku koja je zajednička za krivu i tangentu i da imaju isti nagib...

Možemo li iz ovoga zaključiti da se dve tačke (jedna na pravoj a druga na krivoj) ne mogu dodirivati?

Znači da je smisao pojma "dodirivati" to da imaju zajedničku tačku. Slično kao što kriva i prava mogu imati zajedničku tačku ako se seku, e pa tangenta i kriva se ne seku nego "dodiruju". Imaju zajedničku tačku i to tačno jednu. Dve različite tačke se nikada ne dodiruju - ne postoji neko rastojanje između bilo koje dve tačke, a u koje ne može da se ugura još neka tačka (u srtvari beskonačno mnogo tačaka).

Prava i kriva koje se seku takodje mogu imati zajednicku tacku i to tacno jednu.
Tangenta na krivu moze imati vise od jedne zajednicke tacke sa tom krivom.
Bitan je deo da u tacki koja im je zajednicka imaju isti nagib.

Pretpostavimo da je kriva crvene boje kao i konveksna površina koju ta kriva ograničava.
Pretpostavimo takođe da je tangenta plave boje kao i jedna poluravan koju ta prava ograničava.
Pretpostavimo takođe da se te površine nigde ne preklapaju već se samo dodiruju u jednoj tački.
Koje boje je ta "zajednička" tačka?

_{[Ovu poruku je menjao Diskriminanta dana 16.07.2016. u 20:59 GMT+1]}

To crveno i plavo sto imas na slici su povrsine a ne kriva i prava linija.

Ljubičaste?

Nisi pažljivo pročitao moju prethodnu poruku, linije su tu, nisu se izgubile.

Dužine su ograničene tačkama, površine linijama, prostori ravnima ukoliko nisu beskonačni na sve strane.

Ali ljubičasta je nastala od dve boje odnosno od dve tačke različitih boja kada su na istom mestu.
To bi nekako i moglo da prođe, ali kako tačka može imati boju kad nema površinu?

Ako je neka površina skup takvih tačaka onda ni površina ne može imati boju.

Bezbojna? :)

Citat: Diskriminanta:

"Ali ljubičasta je nastala od dve boje odnosno od dve tačke različitih boja kada su na istom mestu.
To bi nekako i moglo da prođe, ali kako tačka može imati boju kad nema površinu?

Ako je neka površina skup takvih tačaka onda ni površina ne može imati boju."

Pa ti si ih prvi ofarbao? Iako nemaju odgovarajuću dimenziju za farbanje?

Citat: Diskriminanta:

"Pretpostavimo da je kriva crvene boje kao i konveksna površina koju ta kriva ograničava.
Pretpostavimo takođe da je tangenta plave boje kao i jedna poluravan koju ta prava ograničava."

Mslm, kako prava može biti neke boje ako nema dimenziju što se zove širina već samo dužinu ili tako nekako?

Upravo tako! Ali nije važno ko ih je "ofarbao". Važno je da je to nemoguće kad su u pitanju tačke i linije,
međutim, nikom to nije zasmetalo.
Pa ni sada nikom ne smeta to što neka površina može biti crvene boje iako ni jedna njena tačka ne može.
Kako to objašnjavaš?

Mislim da su u pitanju apstrahtni pojmovi, pa kako u realnosti ne postoje, ne mogu postojati ni njihove boje niti se mogu obojiti, a ako ih zamislimo možemo zamisliti u kojoj hoćeš boji pa i šarene.

A ako je pitanje kako da to nikom nije zasmetalo, pa eto ljudi su tolerantni? :)

I površine i boje su realni pojmovi.

Realne pojmove ne možemo objašnjavati proizvoljnim apstrakcijama, a što se tiče tolerancije
ona je nedopustiva u ozbiljnoj analizi.

Ja namerno nisam odgovorio na tvoje glupo pitanje o bojama.

Ali recimo da ovako postavimo problem.

Neka je P skup svih "plavih" tačaka a Q skup svih "crvenih" tačaka. Plava je glupa osobina data tačkama, ali ako kažemo da je iskaz "plava" u stvari iskaz p - tačka pripada puluravni a da je "tačka crvena" ako pripada podskupu tačaka u ravni ispod krive, onda možemo da diskutujemo.

Na mom primeru sa krugom i tangentom skup P = { (x,y) | y>=1 } i Q = { (x,y) | x^2 + y^2 <= 1 }, iskaz p je tačan za (x,y) pripada P i iskaz q je tačan za (x,y) pripada Q.

Tada je za tačku T (0,1) tačno p i q.
To znači da je tačno i da je "tačka plava" i da je "tačka crvena".

Može se napraviti bezbroj ovakvih priča da bi se izveo pogrešan zaključak.
Činjenice su, međutim, sledeće:

1. Tačka ne može imati boju jer nema dimenziju.
2. Konkretno, deo neke ravni ima dimenziju površine pa može imati boju -
prema tome - ravan ili njen deo nije skup bezdimenzionalnih tačaka.

Da, to je opet tvoja besmislena konstrukcija o postojanju praznina.

Boja je fizička osobina materije da absorbuje ili odbija deo elektromagnetnog spektra zračenja koji mi možemo da detektujemo očima i koji zovemo (deo spektra) vidljiva svetlost.

Tačka, prava ravan su matematičke apstrakcije koje nemaju fizički ekvivalent.

Daću ti još jedan primer kojeg se sećam sa početka predavanje o elektromagnetici i Maksvelovim jednačinama.

Pisac udžbenika je posvetio nekoliko paragrafa ograničenjima Maksvelovih jednačina. Pošto se tu radi o integralima i diferencijalima nekih funkcija, vrlo jasno nam je rekao da ne razmišljamo o MATEMATIČKIM apstrakcijama nego na konkretan, fizički način. Recimo, ako se u formuli pojavljuje dV (elementarna zapremina), rekao je, shvatite to kao 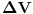, a ta zapremina je, u stvari zapremina dovoljne veličine da u nju stane milijardu atoma, ili neki drugi veliki broj, ili da to shvatim kao 1 kubni milimetar. Nije bitno. Bitno je da dV ne shvatimo kao matematički dV nego kao fizički.

Dakle, matematika je apstrakcija, sa svojim pravilima. Fizika radi sa konačnim veličinama.

Varaš se! Ni matematika ne može tvrditi nešto što iz njenih zakonitosti ne sledi.

To ne može sve i da hoće. Ahahaha :)

Pa zašto onda tvrdiš suprotno?



Niste dali prihvatljivo objašnjenje.



_{[Ovu poruku je menjao Diskriminanta dana 19.07.2016. u 10:54 GMT+1]}

@Diskriminanta
Presek dva skupa A i B je skup koji sadrzi sve elemente skupa A koji pripadaju i skupu B, odnosno koji sadrze sve elemente skupa B koji pripadaju i skupu A.
To je odgovor na sva tvoja pitanja.

Pogledaj naslov teme!

Nezgodacija je u tome što kad napišeš nešto kao "Pa zašto onda tvrdiš suprotno?" ok bi bilo da citiraš gde ja to tvrdim suprotno (na stranu sad to što ja trenutno nemam pojma suprotno u odnosu na šta, čega, ili u odnosu na kakvu izjavu ti uopšte misliš), medjutim posle "Pa zašto onda tvrdiš suprotno?" ti citiraš sam sebe gde konstatuješ da nikome ne smeta što skup nekih entiteta može imati neku osobinu koju nijedan od pojedinačnih entiteta tog skupa samostalno ne može imati. Tjah, bivol je prilično plašljiva životinja, biljojed i sam se nikad ne bi suprotstavio čoporu lavova, medjutim krdo bivola ume što da se suprotstavi čoporu lavova, što da odbrani mladunca, što da ugazi i utepa lava, tako da...skup bivola ima neku osobinu koju pojedinačni bivol nema, tako i skup tačaka, površina može imati neku osobinu da je crvene boje iako ni jedna njena tačka ne može imati tu osobinu na primer. Ja i dalje tvrdim da biologija ne može tvrditi nešto što iz njenih zakonitosti ne sledi. Isto važi i za matematiku, itd...

Ako neku konačnu obojenu površinu podeliš makazama na nekoliko delova onda će i svaki taj deo imati i površinu i boju.
Taj postupak možeš nastaviti tako da opet svaki taj deo podeliš na nekoliko delova i opet će ti delovi imati
dimenziju površine recimo u m² i istu boju.
Taj postupak možeš nastaviti u beskonačnost, ali ni dimenzija ni boja beskonačno malih delova dobijenih takvim
postupkom neće nestati.

Te beskonačno male delove površine možemo označiti sa nulom, ali ta nula ima dimenziju izraženu u m²
Zašto?
Zato što obrnutim postupkom t. j. sastavljanjem tih delova odnosno množenjem sa beskonačno možeš dobiti početnu
površinu koja će imati dimenziju u m² i, naravno, boju.

Nulu koja nema dimenziju možeš množiti sa beskonačno ali ne možeš na taj način dobiti dimenziju jer bi to bilo
stvaranje nečega iz ničega.

Ništa što postoji ne može se uništiti niti se išta što ne postoji može stvoriti.
Može samo da se menja vid postojanja

Dakle beskonačno ne uništava dimenziju niti je stvara.
Beskonačno ne može uništiti ni površinu ni boju, kao što ih ne može ni stvoriti.

Ispravno je F[m²]/∞ = 0[m²], a ne F[m²]/∞ = 0

Nula bez dimenzije se ne može dobiti deljenjem veličine koja ima dimenziju

Ajde da uzmemo makaze i seckamo papir A0 formata, tako da svaki put presečemo na pola. I neka je taj papir CRVENE boje. Talasna dužina crvene svetlosti je 700nm, pa neka zaokružimo na 1000 nm, odnosno 10^-6 m. Da bi neki predmet bio vidljiv u crvenom spektra, mora da bude veći od talasne dužine crvene svetlosti. Dakle, vidljivi deo papira bi morao imati površinu od 10^-12 m2. Papir A0 ima površinu od 1m2. Seckanjem na pola, posle 36 seckanja dolazimo na površinu koja više nije crvena. Dakle, značajno manje od beskonačnog broja seckanja. Neka mi nastavimo i dalje sa seckanjem. Posle 54 seckanja više nemamo ni papir, došli smo do toga da smo iseckali molekule celuloze na pojedinačne molekule glukoze. Nekoliko seckanja posle toga došli smo na nivo atoma i dalje nema seckanja...

U matematici, možemo i dalje da seckamo. Bolje prouči kako radi prostata nego da se baviš Euklidskom geometrijom. Jer to je najviše sa čime nekako i barataš. Matematika od 17. veka pa do danas ti je totalna nepoznanica.

Šta tebi vredi poznavanje matematike kad s logikom kuburiš. Poznavanje i razumevanje su dve različite stvari.

Pokušaj da oboriš ovaj moj zaključak:

Deoba na beskonačno mnogo delova ne uništava dimenziju niti se iz zamišljenih elemenata bez dimenzije može stvoriti dimenzija ni na koji način.

Beskonačnost nije ni generator ni eliminator dimenzije

@Diskriminanta
Da bi uopste mogao da zahtevas da ti neko obori "zakljucak", moras prvo da definises pojmove koje koristis u "zakljucku":
- deoba
- beskonacno
- mnogo
- deo
- unistiti
- dimenzija
- zamisljen
- element
- stvoriti

Tek onda mozes od nekog ocekivati da ulazi u diskusiju sa tobom i obara ili potvrdjuje tvoje "zakljucke". Posto se pozivas na logiku, bilo bi dobro da definises logicki skup aksioma, tvrdjenja i definicija koje koristis prilikom gradjenja "zakljucka".

@Diskriminanta Svaki tvoj iskaz je toliko šupalj da odzvanja glupošću nadaleko.

Evo, ja ću da podelim beskonačan skup na samo dva dela i uništiću dimenziju. Neka je prava p skup tačaka u realnoj ravni za koje važi da je koordinata tačaka koje pripadaju pravoj y=x. Podeliću skup tačaka na samo dva podskupa podskup P={(0,0)} i Q{(x,x) | x <> 0 }. Eto - moj skup P ima samo jedan bezdimenzioni element koji sam dobio od jednodimenzionalnog geomerijskog objekta.

Od sada možeš da mi se obračaš sa: O, Veliki Generatore I Uništitelju Dimenzija.

U pavu si, ali to možeš i sam da uradiš ako si razumeo, a ako nisi i to ti je džabe.

Nisi ti uradio ama baš ništa. Prava nije skup bezdimenzionalnih tačaka.
Možeš ti nanizati u svojoj glavi beskonačan skup takvih tačaka kakav ti drago, ali nećeš dobiti pravu niti bilo koliki njen deo.
Ne može se od tačaka koje nemaju dimenziju formirati prava niti ma koliki njen deo koji imaju dimenziju.

Ti si se uživeo u ulogu Stvoritelja. Stvaraš iz ništa nešto.

Beskonačno mali deo prave ima jednu dimenziju, stoga tvoje bezdimenzionalne tačke ne pripadaju pravoj.

1 Aksiome incidencije:
I.1 Svaka prava sadrži najmanje dve tačke A i B.
I.2 Postoji najmanje jedna prava koja sadrži dve tačke A i B.
I.3 Postoji najviše jedna prava koja sadrži dve razne tačke A i B.
I.4 Svaka ravan sadrži najmanje tri nekolinearne tačke A, B, i C.
I.5 Postoji najmanje jedna ravan koja sadrži tri tačke A, B i C.
I.6 Postoji najviše jedna ravan koja sadrži tri nekolinearne tačke A, B i C.
I.7 Ako dve razne tačke A i B neke prave p preipadaju nekoj ravni π, tada
sve tačke prave p pripadaju ravni π.
I.8 Ako dve ravni α i β imaju zajedničku tačku A, onda one imaju najmanje
još jednu zajedničku tačku B.
I.9 Postoje četiri nekomplanarne tačke A, B, C, D


Ovo su početne aksiome Euklidske geometrije.

Izvoli pa formuliši svoju geometriju. Posebno obrati pažnju na 7. aksiomu i definiši šta to čini pravu u tvojoj geometriji.

Inače, ovo je geometrija za 3. razred srednje škole (matematičkog usmerenja). Tvoje znanje je podskup znanja učenika 2. razreda srednje škole...

Tačka ne pripada ničemu. Tačka je mesto u prostoru, na nekoj ravni ili na nekoj pravoj.
odnosno tačka se nalazi kao neko mesto u prostoru, ravan može prolaziti kroz to mesto, prava može prolaziti kroz to mesto.
Tačka je nezavisno mesto u prostoru.

Aksiome incidencije trebalo bi da glase:
1. Svaka prava prolazi kroz najmanje dva mesta A i B
2. Postoji najmanje jedna prava koja prolazi kroz dva mesta A i B
3. Postoji najviše jedna prava koja prolazi kroz dva razna mesta A i B
4. Svaka ravan sadrži najmanje tri nekolinearna mesta A, B i C
5. Postoji najmanje jedna ravan koja sadrži mesta A, B i C
6. Postoji najviše jedna ravan koja sadrži tri nekolinearna mesta A, B i C
7. Ako prava p prolazi kroz dva razna mesta A i B kroz koje prolazi i ravan π
tada kroz sva mesta kroz koja prolazi prava p prolazi i ravan π
8. Ako dve ravni α i β prolaze kroz zajedničko mesto A onda one prolaze kroz najmanje još jedno zajedničko mesto B.
9. Postoje četiri nekomplanarna mesta A, B, C, D.



Prava je beskonačan skup beskonačno malih kontinualnih intervala koji imaju dimenziju dužine.



Ne brini o mom znanju, bolje bi bilo da malo više posvetiš pažnju svom razmišljanju.

Osim što si zamenio reč tačka rečju mesto, nisi ništa izmenio u aksiomama. Uveo si pojam "malih kontinualnih intervala" koji ništa ne znači.

Ako je tvoje razmišljanje odgovor, šta je pitanje? Šta tvoje "razmišljanje" menja u geometriji. Samo da napomenem, ove (i ostale aksiome Euklidske geometrije) matematičari su pokušali da prošire ili smanje poslednjih 2000 godina i nisu našli ni jednu viška ni jednu manjka da bi napravili bolji sistem, osim što su izmenom aksioma paralelnosti uspeli da naprave neeuklidksku geometriju.

Samo prazno blebetanje...

Ne znači ništa za one koji ne misle. Beskonačnim deljenjem kontinuuma ne možeš dobiti delove koji nemaju dimenziju
jer bi to značilo uništenje kontinuuma, a to nije moguće.
Aksiomama ništa ne fali izuzev što su mesta nazvana tačkama i dodata geometrijskim pojmovima kao njihov deo
što nije istina. Tačka i kontinuum su dve različite stvari, a kontinuum se uzalud pokušava objasniti tačkama bez dimenzije.
Usitnjavanje kontinuuma do beskonačno malih veličina ne uništava svojstvo dimenzije tih veličina - one ne postaju tačke bez dimenzije.
Svaki deo kontinuuma, ma koliki on bio, je opet kontinuum.

I to tvoje!

Kako elegantno izbegavaš da uletiš u diskusiju, jer znaš da ne možeš da pobediš. Lepo sam te zamolio da definišeš pojmove, a ti izbegavaš. Na taj način možeš da diskutuješ o svemu i da iz bilo čega zaključuješ bilo šta. Dokle god precizno ne definišeš sve pojmove kojima gradiš svoju teoriju, svaka buduća diskusija je gubljenje vremena.

Razumem da si amater, ali ti čak ni ne želiš da prevaziđeš amaterizam. Dokle god ne budeš razumeo pojam neprekidnosti, tebi nema pomoći. Na kraju krajeva, s obzirom da je ova tema završila na elitemadzone gde joj je i mesto, isključujem se iz ovog gubljenja vremena.

Pozdrav i srećno.

Diskriminanta,

Danas sam išao do grada da platim neke račune, međutim u povratku sam se setio jedne poznate priče. Ona kaže sledeće: da bih se vratio kući, trebalo bi da najpre pređem polovinu puta, a da bih prešao tu polovinu, najpre moram da pređem njenu polovinu. Međutim, da bih prešao tu polovinu, morao bih da pređem polovinu te polovine,... Eto, pošto nema šanse da se vratim kući, seo sam u baštu i pijem sok. Nemoj samo da me pitaš kako sam došao od kuće do grada.

P.S. Jei li nekada učio malo matematike, limesa, integrala?

Može, može.

https://en.wikipedia.org/wiki/...7s_paradoxes#Dichotomy_paradox

Mada meni lepša kornjača

https://en.wikipedia.org/wiki/...oxes#Achilles_and_the_tortoise