[ misham @ 16.04.2008. 06:19 ] @
| zna li neko neku dobru knjigu iz ove oblasti (a da nije Luciceva euklidska i hiperbolicka geom.) u kojoj se uvodi i odrdjivanje razdaljine izmedju dve tacke. |
|
[ misham @ 16.04.2008. 06:19 ] @
[ Nedeljko @ 17.04.2008. 13:53 ] @
U poluravanskom modelu hiperbolicke geometrije
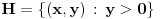 rastojanje beskonacno bliskih tacaka rastojanje beskonacno bliskih tacaka 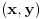 i i 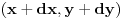 se definise kao se definise kao 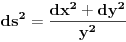 . Slicno, u poluprostornom modelu hiperbolicke geometrije . Slicno, u poluprostornom modelu hiperbolicke geometrije 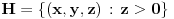 rastojanje beskonacno bliskih tacaka rastojanje beskonacno bliskih tacaka 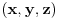 i i 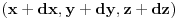 se definise kao se definise kao 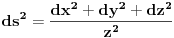 . To znaci da se duzina luka . To znaci da se duzina luka 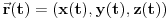 gde gde 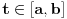 izracunava po formuli izracunava po formuli 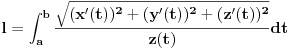 . Obzirom da znas sta je u tom modelu duz sa datim krajevima, mozes da izracunas rastojanje od proizvoljne dve tacke. . Obzirom da znas sta je u tom modelu duz sa datim krajevima, mozes da izracunas rastojanje od proizvoljne dve tacke.[ misham @ 20.04.2008. 15:48 ] @
A iz koje si knjige to naucio posto me ne interesuje samo poluravanski model, vec i disk model i klajnov model, a i interesuju me i neke druge krive?
I da te pitam sta je to tenzor(tenzorski racun), posto je znam samo to da je on kao neka "nadogradnja" vektorskog i skalarnog racuna? I samo, hiperbolicke f-je koje se uce(spominju) u srednjoj skoli, da li imaju veze sa trigonometrijom hiperbolicke geometrije? [ Nedeljko @ 20.04.2008. 19:15 ] @
Citat: misham: A iz koje si knjige to naucio "Diferencijalna geometrija" autora Nede Bokan i pokojnog Novice Blažića. Citat: misham: I da te pitam sta je to tenzor(tenzorski racun), posto je znam samo to da je on kao neka "nadogradnja" vektorskog i skalarnog racuna? U istoj knjizi imaš definiciju tenzora na Rimanovoj mnogostrukosti. Citat: misham: I samo, hiperbolicke f-je koje se uce(spominju) u srednjoj skoli, da li imaju veze sa trigonometrijom hiperbolicke geometrije? Formule sferne trigonometrije prelaze u formule hiperboličke planimetrije tako što trigonometrijske funkcije prelaze u odgovarajuće hiperboličke trigonometrijske funkcije. No, naziv "hiperboličke funkcije" je stariji i ima sasvim drugo poreklo. [ misham @ 20.04.2008. 21:00 ] @
pa sad, sta je to mnogostrukost? :)
je li to prostor, ili nesto drugo? [ Nedeljko @ 21.04.2008. 10:56 ] @
U knizi imas definiciju mnogostrukosti. No, tamo nemas Klajnov disk model, niti Poenkareov disk mode, ali se i njihove metrike mogu lako izracunati.
[ Nedeljko @ 22.04.2008. 10:31 ] @
[ misham @ 22.04.2008. 13:50 ] @
hvala
[ Sonec @ 07.06.2012. 17:32 ] @
Ako sam ja dobro razumeo, da li se ovako racuna rastojanje izmedju tacaka
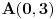 i i 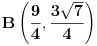 u poluravanskom modelu u poluravanskom modelu  hiperbolicke geometrije sa prvom formom hiperbolicke geometrije sa prvom formom 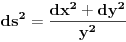 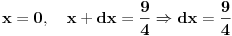 , i slicno , i slicno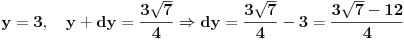 Pa je 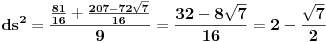 , odnosno , odnosno 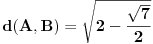 . .Jel valja ovo? I da pitam jos ovo, ako su mi date dve tacke, da li mogu da znam kako izgleda jednacina prave koja prolazi kroz te dve tacke? (u pitanju je isti model hiperbolicke geometrije, ista metrika) [ Nedeljko @ 07.06.2012. 19:54 ] @
Pa, valjda se zna šta su u tom modelu prave i samim tim koja prolazi kroz dve date tačke.
Što se rastojanja tiče, ne valja ti račun, jer je 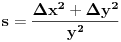 samo za "beskonačno bliske tačke". Zapravo, ta metrika znači da ako ti je data kriva samo za "beskonačno bliske tačke". Zapravo, ta metrika znači da ako ti je data kriva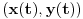 , , 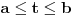 , ,onda je njena dužina 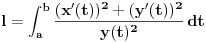 . .E, sad, rastojanje tačaka se računa kao infimum dužina svih lukova koji spajaju te dve tačke. U ovom modelu postoji tačno jedan najkraći put između dve tačke, tj. duž određena tim tačkama, pa je hiperboličko rastojanje između dve tačke u ovom modelu dužina hiperboličke duži koja povezuje te dve tačke računata po gornjoj formuli. [ Sonec @ 07.06.2012. 20:46 ] @
Ja na primer znam kako da nadjem rastojanje izmedju tacaka
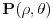 i i 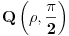 (datih u polarnom obliku, (datih u polarnom obliku, 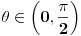 ). Naime, najmanje rastojanje izmedju njih se realizuje po polukrugu sa centrom ). Naime, najmanje rastojanje izmedju njih se realizuje po polukrugu sa centrom 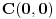 i poluprecnika i poluprecnika  . .Prava koja prolazi kroz ove dve tacke i preko koje se realizuje najkrace rastojanje je 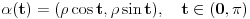 , pa je , pa je 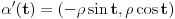 . S obzirom na datu metriku, . S obzirom na datu metriku, 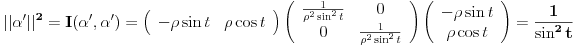 , odnosno , odnosno 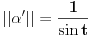 Pa je samim tim 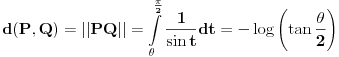 To je u sustini (kada ne bih radio sa konkretnim vrednostima) koliko ja vidim ista formula koju si i ti dao (samo sa korenom), koja mi do sada nije bila poznata. Citat: Nedeljko: Pa, valjda se zna šta su u tom modelu prave i samim tim koja prolazi kroz dve date tačke. E, ovo mene interesuje. Bio bih ti zahvalan za malo objasnjenje. [Ovu poruku je menjao Sonec dana 07.06.2012. u 23:01 GMT+1] [ Nedeljko @ 08.06.2012. 00:04 ] @
Pa, ako imaju istu x koordinatu, onda je to poluprava normalna na apsolutu, a u suprotnom polukrug čiji je centar presek apsolute i simetrale euklidske duži određene tim tačkama.
[ Sonec @ 08.06.2012. 00:17 ] @
Hvali ti mnogo! Ovaj polukrug me je nervirao, nisam znao kako da mu nadjem centar, a zaboravljao sam da mu centar mora pripadati apsoluti.
To je ono kad covek pocne bespotrebno da komplikuje stvari i ne veruje da postoji lako resenje. Upozoravali su nas na to na fakultetu, nisam verovao, al izgleda da je pocelo da se ostvaruje. Hvala jos jednom. [ ortodox888 @ 11.06.2012. 20:05 ] @
Nedeljko može pomoć oko jednog zadatka (bio na ispitu, danas). Date tri tačke u poluravanskom modelu hiperboličke geometrije i treba da nađemo hiperboličku jednačinu kruga koji sadrži te tri tačke. Ja sam uspeo da nađem hiperbolički centar i prečnik ali do jednačine ni makac.
[ Nedeljko @ 11.06.2012. 20:29 ] @
Nije mi jasno kako ne možeš na osnovu centra i poluprečnika da napišeš jednačinu kruga.
Ako treba dati jednačinu nečega, to je moguće samo u koordinatnom sistemu. Za to mogu poslužiti euklidske koordinate hiperboličkih tačaka. U tom slučaju, pošto je hiperbolički krug uvek euklidski krug (samo što mu hiperbolički centar nije isto što i euklidski centar) dovoljno je da nađeš euklidski krug koji sadrži te tri tačke i njegovu euklidsku jednačinu. Ako ste koristili neki drugi koordinatni sistem, onda napiši koji je sistem u pitanju. [ ortodox888 @ 11.06.2012. 21:12 ] @
Samo da razgraničimo: Znači za jednačinu hiperboličkog kruga je dovoljno naći euklidski centar i euklidski poluprečnik, tj nisu mi potrebni ni h-centar ni h-poluprečnik?
[ Nedeljko @ 11.06.2012. 21:52 ] @
Pa, ako su koordinate h-tačaka euklidske koordinate modela, onda je tako.
[ ortodox888 @ 12.06.2012. 09:04 ] @
Hvala puno. Sad shvatam koliko sam isp`o glup.
[ Nedeljko @ 12.06.2012. 10:01 ] @
Nisi glup, nego je to trik zadatak.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|