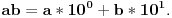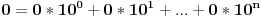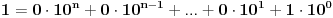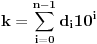|
|
[ uciteljicaana @ 15.12.2011. 16:37 ] @
|
| Imam problem da definisem nulu u nizim razredim OS. Naime, prvo je bio problem da li je nula uopste broj, i to smo rarazjasnili jer u metodici jasno pise da je nula broj koji pripada skupu N-nula. Pretpostavljam - po zdravoj logici - da je nula jednocifren broj ( a zasto ne bi bio? - ima jednu cifru! ) ali to ne mogu da dokazem kolegama koji tvrde da nula jeste cifra ali ne i jednocifren broj. Moze li mi ko pomoci oko dileme, eventualno da navede neku strucnu literaturu u prilog moje ili njihove tvrdnje? Hvala! |
[ SrdjanR271 @ 15.12.2011. 18:00 ] @
Npr. dvocifren broj 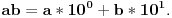
Nula može tom logikom da bude n-tocifren broj.
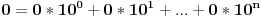 [ Sini82 @ 15.12.2011. 20:22 ] @
@SrdjanR271
I broj 1 tom logikom može biti n-tocifren broj:
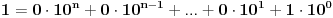 .
U zapisu broja nula (0) koristi se jedna cifra; u zapisu broja sto (100) tri cifre itd.
@uciteljicaana
Nula jeste broj. Ako ne znate kako da ga uvedete, imam prijedlog:
-neka vam jedan ucenik napiše na tabli broj klupa u učionici;
-drugi broj prozora itd.
-neka u sveske zapišu koliko ima lustera u učionici itd.
-nakon toga neka zapišu koliko ima stogodišnjaka u učionici, uvedite simbolički zapis 0, objasnite da je i to broj, ispričajte im o istoriji nule;
-neka sami navode primjere.
Budite kreativni, možda vam sljedeći linkovi pomognu da sami shvatite malo bolje šta je nula:
https://docs.google.com/viewer...tbQQivCEcxBiiA76n-gOA_Tj4rNKnw
http://static.astronomija.co.r...iji/B92/2008/novembar/Nula.htm
http://www.creemaginet.com/sajt/node/2072
[Ovu poruku je menjao Sini82 dana 15.12.2011. u 21:36 GMT+1]
[ X Files @ 15.12.2011. 20:46 ] @
Ovo pitanje sam i ja ranije hteo da postavim, jer sam roditelj detata koje je sada II razred OŠ.
U udžbenicima Kreativnog centra za I razred OŠ, nigde eksplicitno se ne navodi "koji je najmanji jednocifreni broj", iako se u zadacima često traži kao jedan od podataka.
Oni su to ovako rešili:
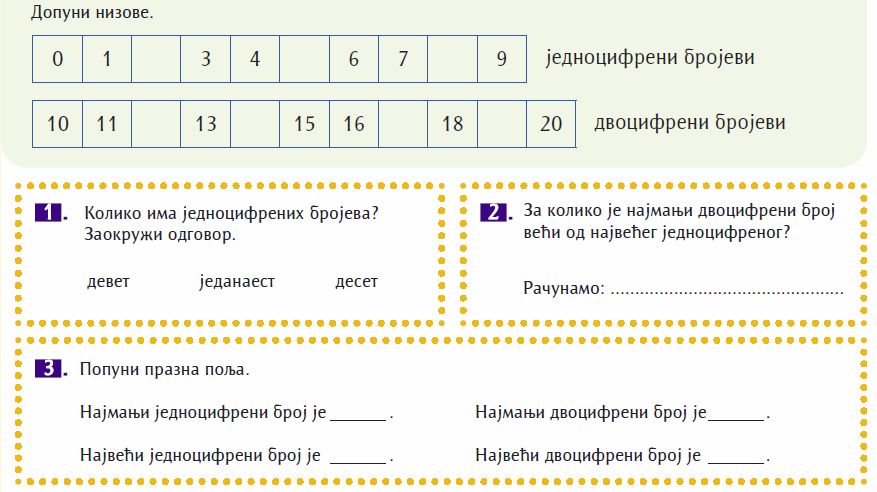
Sa slike se zaključuje da nula jeste cifra, i to najmanja jednocifrena. Takođe se uzima i za "najmanji jednocifreni broj". Da ne ulazimo u to šta je -9, šta su prirodni brojevi, i sl. :)
Nasuprot tome, situacija je čista ako se pominju brojevi PRVE desetice (1, ..., 10), DRUGE desetice (11, ..., 20), itd. Tada se jasno zna koji je "najmanji broj prve desetice".
Ukratko, ako se u zadatku spomene kao reč ili deo reči "cifra", uračunaj i nulu. Ako se spominju desetice, nulu zaboravi. Ako se ne varam, ovakva postavka stvari se može pronaći i u zadacima Arhimedesa za niže uzraste.
Inače, ja sam dilemu presekao ovim zadatkom (tj, njegovim rešenjem), jer je autor jedan od većih autoriteta u ovom domenu:
Zadatak:

Posle svih tih dilema, kada sam video ovaj zadatak, rekao sam sebi (okrećući listove da pogeldam rešenje) - "ako Mioljub bude rekao da je rešenje NULA, onda je najmanji 'jednocifreni broj' nula i tačka" :)
Rešenje:

[ nikolinv @ 15.12.2011. 21:05 ] @
Sve zavisi kako gledaš na "problem nule". Situacija je otprilike ovakva:
1. Ako gledaš striktno matematički, da ne kažem naučno (akademski), nema smetnji da nula bude prirodni broj. Npr. u Peanovim aksiomama ćeš naći nulu kao osnovni, početni element skupa N i jedinu konstantu.Sve ostale brojeve on dobija preko nule. Sve se lepo slaže imaš kod Peana sledeće:
a) n + 0 = n , n pripada N, jedinični element strukture (N, +)
b) n * 0 = 0 , n pripada N slično za *
c) Indukcija kreće od nule
d) 0'<>0
Moglo bi se reći da nula ima čvrsto algebarsko uporište.
2. Kako ti ne radiš sa studentima, već sa osnovcima, tu se koristi do sada jedna jedina poprilično falična metodička teorija (zašto je falična neću sada o tome, ali bolje nemamo) a to je Hekelov biogenetski zakon (teoriju rekapitulacije): individualno razviće organizma (ontogenija) je rekapitulacija njegovog evolucionog razvića (filogenije).
To konkretno znači da nam je istorija matematike glavna vodilja kroz razvoj jedinke (učenika). Zato ti je vrsnije da čitaš članke iz istorije matematike nego neku stručnu literaturu. Kako se u početnoj fazi razvoja matematike javlja "problem nule" (stari narodi dugo nisu imali oznaku za nulu, pa su operacije sa prirodnim brojevima bile prilično komplikovane) nula se uvodi u školu kasnije, ne na početku.
Elem, prirodni brojevi se uvode kao oni brojevi koje koristimo za brojanje: 1,2,3... Nema još nule. Daj đacima problem: "Imaš tri jabuke, ja ti uzmem tri. Koliko ti ostane?" i ko ti odgovori "nula" slobodno mu daj peticu - nećeš pogrešiti. Očekivan odgovor je "ništa". O tome se radi, ja insistiram na tome da je ništa kod brojeva nula, a kod skupova je to prazan skup.
Nulu možeš definisati kao broj koji dodat bilo kom drugom broju daje taj broj, mada nema za tim ni potrebe na početnom nivou.
Nadam se da sad bolje razumeš ovu anomaliju sa nulom, ovo je inače najčešće pitanje koje čujem od učiteljica.
Pozdrav.
[ uciteljicaana @ 15.12.2011. 22:38 ] @
X Files je u pravu sto se tice udzbenika iz matematike. Kreativni centar nije jedini udzbenik koji ima dilemu sa nulom koju provlaci kroz zadatke gde je resenje nejasno. Kao uciteljica imam skromno znanje iz matematike i sto se 1-4. razreda tice stvari stoje ovako: prirodni brojevi su svi celi brojevi od jedan pa nadalje... svaki prirodan broj ima svog prvog prethodnika osim jedinice ( nula dakle nije prirodan broj ) itd. Nula se u nizim razredima izucava kao broj i to nije sporno i prirodni brojevi sa nulom cine skup N nula. S obzirom da se nula uci obicno posle broja pet ( kao broj koji oznacava prazan skup ili razlika dva ista broja ) dakle u pocetku 1. razreda logicno je zakluciti da ucenici u startu barataju skupom N nula ( iako se njima u toj fazi ne objasnjava sta su prirodni brojevi a sta N nula skup ). To navodi na zaklucak da kada se postavi pitanje koji je najmanji jednocifren broj - ucenici odaberu najmanji jednocifren broj od nauceni brojeva - dakle nula. Po mojoj logici stvari izgledaju ovako: - nula je broj, brojevi sa jednom cifrom su jednocifreni brojevi,zakljucak-nula je jednocifren broj. Pitanje - gde to eksplicitno pise da je nula jednocifren broj - cisto da se ne oslanjam argumentacijom samo na svoju logiku?! Valjda ima neke valjane literature koja o tome u matematici govori, mozda skup celih brojeva, gde bi opt, po mojoj logici u tom skupu najmanji jednocifren broj trebao biti -9?
I jos nesto - na kog Mioljuba mislite, mozda mogu da pronadjem njegovu metodiku i u kom udzbeniku se nalazi onaj 11. zadatak?
[Ovu poruku je menjao uciteljicaana dana 16.12.2011. u 00:00 GMT+1]
[ X Files @ 16.12.2011. 09:56 ] @
Slučajno sam pronašao na netu deo neke zbirke:
Mioljub Isailović
ZANIMLJIVA MATEMATIKA
Zbirka zadataka za učenike II razreda osnovne škole
Šabac, 2000
(Emailom sam ih kontaktirao da bih je kupio, ali izgleda da je tiraž bio premali)
To nije klasična zbirka zadataka za II razred i puno razlikuje se od "običnih" zbirki. Ne bih da budem zlurad, ali zbirka je teška i za prosečnog roditelja.
"Obične" zbirke su namenjene takozvanom "srednjem učeniku". Taj srednji učenik za nedelju dana shvati tip zadataka i kasnije se sve vrti u krug (Milica, Ana, Marija, ... "za toliko više od Ane", "toliko puta manje od Marije), samo se menjaju imena i brojevi. To vodi utvrđivanju materijalnih znanja, na štetu funkcionalnih znanja i logičkog mišljenja. Na primer, čim se zadatak malo "okrene" rečima (dovoljno je da se polazni podatak nalazi tek na kraju teksta zadatka), dete koje bez ikakvih problema rešava one zadatke iz običnih zbirki - blokira, jer nije naučeno da razmišlja.
Ta zbirka učenika tera da koristi olovku za "razmišljanje", pre nego što se dođe u poziciju da se zadatak reši. Zadaci su raznovrsni. Ima dosta korisnih tehnika na kojima se insistira, na primer na "metodi lažne pretpostavke", "metodi dužina". Posle par baš takvih zadataka (metoda lažne pretpostavke) koje sam sopstvenom detetu razjasnio, primetio sam da dete često ovu metodu koristi i za druge zadatake, što me je oduševilo. To je prava stvar, kada se uveriš da dete stečena znanja usvaja kao trajnu intelektualnu svojinu i koristi ih u drugim situacijama.
Možda ne bi bilo loše na kontrolnim zadacima, kao poslednji zadatak (koji se ne ocenjuje negativno) dati i neki iz ovakve zbirke.
Sada sam malo skrenuo s teme, ali nije zgorega. Nema baš puno tema koje se tiču metodike matematike za niže razrede OŠ.
Citat: Kao uciteljica imam skromno znanje iz matematike
Hvala Bogu da ima nekoga ko zna koliko ne zna :) Ovo naravno nije kritika već pohvala, jer ovako nešto izjavljuje samo neko ko je dovoljno odgovoran i temeljan, što se vidi i po naslovu teme. [ Sini82 @ 16.12.2011. 12:40 ] @
@uciteljicaana
Citat: http://issuu.com/kreativnicentar/docs/matematika-1---udzbenik/search?q=jednocifren (str. 74.):
Znake za pisanje brojeva 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 nazivamo cifre.
Brojevi koji se pišu jednom cifrom jesu jednocifreni brojevi.
Prema tome, nula jeste jednocifren broj.
[ Nedeljko @ 16.12.2011. 14:01 ] @
X Files
Status nule je u ovom slučaju konvencija. Međutim, obzirom da si dobar programer, probaj da napišeš program za ispis broja, pa vidi šta će da ispiše ako nulu ne tretiraš posebno.
Recimo:
Code:
void print(int x)
{
if (x < 0)
{
x = -x;
cout << "-";
}
short c[50];
int i;
for (i = 0; x > 0; x /= 10, ++i)
{
c[i] = x%10;
}
while (i > 0)
{
--i;
cout << c[i];
}
}
Naravno da se funkcija može napisati i rekurzivno bez "anomalije" sa nuklom:
Code:
void print(int x)
{
if (x < 0)
{
cout << "-";
print(-x);
return;
}
if (x >= 10)
{
print(x/10);
}
print(x%10);
}
Međutim, ako se kaže da je broj   -tocifrena ako se može zapisati u obliku
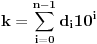
za neke 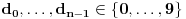 , pri čemu je 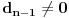 , onda ovo za nulu ima smisla samo za 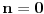 kada indeks po kome se sumira ide od 0 do -1 uz konvenciju da je takva suma jednaka neutralu za sabiranje, tj. nuli.
Hoću da kažem da tretiranje nule kao izuzetka ima smisla. No, u svakom slučaju se radi o konvenciji sa kojom moraju biti usklađeni svi stavovi. Recimo, ako se uči stav da se množenjem broja sa m cifara i broja sa n cifara dobija broj čiji je broj cifara m+n ili m+n-1, onda svakako formulacija stava mora biti u skladu sa korišćenim konvencijama.
No, pošto bi decu sve to zbunjivalo, izabere se jedan sistem i radi se po njemu i priznaju se samo odgovori koji su u skladu sa tim sistemom, pa nauči dete onako kako se u školi traži od njega. [ X Files @ 16.12.2011. 14:13 ] @
Citat: No, pošto bi decu sve to zbunjivalo, izabere se jedan sistem i radi se po njemu i priznaju se samo odgovori koji su u skladu sa tim sistemom, pa nauči dete onako kako se u školi traži od njega.
Da, ovo i jeste suština. Deca do 11 godina su u tzv stadijumu "konkretnih operacija", tako da bi sve sem konvencije bilo pogrešno.
Listajući sve moguće zbirke za ovaj uzrast koje sam našao, zaključio sam sledeće:
* ako se u tekstu zadatka pomene reč cifra ("najmanji jedno cifren broj"), tada u zadatku treba koristiti 0.
* ako se u zadatku kaže "najmanji broj 1. desetice", tada u zadatku treba koristiti 1.
* ako se u zadatku pomene "prvih N" prirodnih brojeva, tada u zadatku treba početi od 1.
Ovo je iskustveno.
P.S. Pogledaću kod koji si ostavio :) [ X Files @ 16.12.2011. 14:18 ] @
@Sini82
[att_img]
Da, ali i ovde nisu smeli da izadju na binu (nego iza, da im izjava ne rikošetira) i kažu "najmanji jednocifreni broj je 0", nego su uveli i pojam "znaci" kao sinonim za cifru :)
[ darkosos @ 16.12.2011. 14:55 ] @
Cifra nije broj :) vec oznaka; shodno tome se moze pitati: koliko si znakova koristio da bi zapisao taj broj? I tako je 0 jednocifren broj.
Npr. 11 je jednocifren broj u heksadecimalnom zapisu jer se pise "B".
[ Nedeljko @ 16.12.2011. 15:20 ] @
Nuli bi matematički mogao da odgovara i prazan string, ali su ljudi odlučili da pišu "0" isto kao što su odlučili da u principu ne pišu vodeće nule, ali da one ako se pojave ne smetaju.
[ X Files @ 16.12.2011. 15:42 ] @
Citat: Cifra nije broj :) vec oznaka; shodno tome se moze pitati: koliko si znakova koristio da bi zapisao taj broj? I tako je 0 jednocifren broj.
Ovo je jasno. Štaviše, cela grupa zadataka za Arhimedes takmičenje se zasniva na distinkciji šta je cifra a šta broj.
Recimo, ovako nekako, "koliko cifara je potrebno za numerisanje adresnih tablica, za 50 kuća jedne ulice".
[ uciteljicaana @ 16.12.2011. 21:11 ] @
Ma, znam ja da u vecini udzbenika za 1. razred ( Atos, Bigz, Kreativni centar ) pise implicitno ili eksplicitno da je nula jednocifren broj i da postoje zadaci kao u KC-u koje je X Fikes navodio... Interesuje me da li postoji neki relevantniji dokaz od udzbenika 1. razreda za to, jer u nekim udzbenicima se navodi da postoji i 9 jednocifrenih brojeva iako je broj nula ucen. Dakle udzbenik nije dokaz u prilog mom stavu. Prosto, ne mogu da poverujem da u matematici ne postoji konkretno objasnjenje ( dok sam isla u skolu mislila sam da matematika bespotrebno objasnjava nesto sto je i isuvise ocigledno, kad gle sada kad mi treba nigde nema objasnjenja?! )
[ Nedeljko @ 16.12.2011. 22:56 ] @
Konvencije se ne dokazuju!
[ igorpet @ 16.12.2011. 23:57 ] @
Citat: X Files: Slučajno sam pronašao na netu deo neke zbirke:
Mioljub Isailović
ZANIMLJIVA MATEMATIKA
Zbirka zadataka za učenike II razreda osnovne škole
Šabac, 2000
(Emailom sam ih kontaktirao da bih je kupio, ali izgleda da je tiraž bio premali)
To nije klasična zbirka zadataka za II razred i puno razlikuje se od "običnih" zbirki. Ne bih da budem zlurad, ali zbirka je teška i za prosečnog roditelja...
Ako te interesuje cela zbirka u elektronskom obliku javi se.
Citat:
0 (nula) je broj, numeral i ime glifa koji predstavlja taj broj. To je ceo broj koji sledi posle broja -1, a prethodi broju 1.
[ nikolinv @ 17.12.2011. 10:29 ] @
Citat: uciteljicaana: Prosto, ne mogu da poverujem da u matematici ne postoji konkretno objasnjenje ( dok sam isla u skolu mislila sam da matematika bespotrebno objasnjava nesto sto je i isuvise ocigledno, kad gle sada kad mi treba nigde nema objasnjenja?! )
Nedeljko je lepo pogodio suštinu jednom rečju - konvencija ili da kažemo dogovor. Pogledajmo nekoliko konvencija:
1. n! = 1*2*3*...*n , n>0, je definicija faktorijela.
Ali imamo i 0! = 1 . Konvencija.
2. x^n = x*x ... *x ( x se pojavljuje na n mesta) je definicija stepena.
x^0 = 1 je konvencija.
x^(-n) = 1/x^n je takođe konvencija.
3. Potraži na ovom forumu post o vrednosti 0^0.
4. (n nad k) = broj podskupova od k elemenata iz skupa od n elemenata.
(n nad 0) = 1 je konvencija.
Sve ove gore navedene konvencije (ima ih još, ovih sam se setio) imaju zajedničku osobinu da se "lepo" uklapaju u date definicije i daju logička proširenja.
Matematika nije svemoguća niti se može meriti sa npr. veronaukom, nemamo explicitan odgovor na svako pitanje. Pogledaj recimo sledeće:
Koliko pravih u ravni prolazi kroz datu tačku van nje i sa njom je paralelno?
Ovo sasvim očigledno pitanje nema odgovor, a neće ga nikada ni dobiti, ali to matematičarima ni najmanje ne smeta i niko sa tim nema problem.
[ since1986BC @ 17.12.2011. 11:26 ] @
I posle neko kaze da staro skolstvo nije valjalo.
[ atelago @ 03.01.2012. 04:47 ] @
Citat: nikolinv: Koliko pravih u ravni prolazi kroz datu tačku van nje i sa njom je paralelno?
Ovo sasvim očigledno pitanje nema odgovor, a neće ga nikada ni dobiti, ali to matematičarima ni najmanje ne smeta i niko sa tim nema problem.
Ovako formulisano pitanje nema odgovor jer na pitanja koja sadrže nemoguće tvrdnje ne može se dati odgovor.
[ Nedeljko @ 03.01.2012. 09:18 ] @
Teba da piše
Citat: Koliko pravih u datoj ravni prolazi kroz datu tačku te ravni, a da ne seče datu te ravni pravu koja ne sadrži tu tačku?
Ovo pitanje zapravo nema smisla. Pitanje npr. o realnim brojevima, a čija formulacija nije ničim vezana za izbor kompletnog uređenog polja ima smisla jer se zna šta su aksiome kompletnog uređenog polja do na ekvivalenciju. Međutim, ne postoji jedinstven do na ekvivalenciju sistem aksioma koji se odnosi na tačke, prave i ravni, tako da je ovo pitanje bez dodatnih informacija jednostavno nedorečeno, baš kao i pitanje da li je realan broj a veći od 3, bez da se kaže na koji se realan broj a misli. Drugim rečima, postavljeno pitanje nema status otvorenog problema, već nedorečenog pitanja, osim ako se misli da se podrazumeva euklidska geometrija ako se izričito ne naglasi drugačije (a obično se misli). [ nikolinv @ 04.01.2012. 13:06 ] @
Citat: Nedeljko: Ovo pitanje zapravo nema smisla.
Zavisi kako za koga, za tebe i mene stvarno nema smsla, ali za nekog ko je ubeđeni 'platonista', ko veruje da prave i ravni stvarno postoje, ovo pitanje i te kako ima smisla. Kako u pitanju i replikama učitiljice provejava realizam, mislio sam da je ovo dobar primer. Isto važi i za pitanje da li je nula prirodan broj ili ne, obe mogućnosti su dozvoljene (ni jedna od te dve mogućnosti ne donosi nikakvu unutrašnju protivrečnost), ne postoji negde u kosmosu pravi skup prirodnih brojeva pa da to pitanje ima jednoznačan odgovor, kao što geometrija, ma koja ona bila, nije geografija univerzuma pa da pitanje petog postulata ima jedinstven odgovor.
Slično, postavimo pitanje da li je matematika prirodna nauka, da li je predmet njenog izučavanja realan svet ili se bavi samo normama i pravilima ali ne i razlozima za nastajanje ili uvođenje tih normi?
Kako bi učiteljica odgovorila na ovo pitanje? [ Nedeljko @ 04.01.2012. 14:46 ] @
Platonista veruje da model euklidske i model hiperboličke geometrije stvarno postoje i ništa više od toga. Ovo pitanje je ekvivalentno pitanju kardinalnog broja grupe. Nisu platonisti baš toliko ludi. Oni zapravo veruju da postoji stvaran svet skupova, sa svim podskupovima skupa prirodnih brojeva i tako dalje kroz hijerarhiju skupova, pri čemu ZFC aksiome izražavaju neke osobine skupova. Gedel je bio platonista ili bar umereni realista, ali nije bio toliko glup da ispituje koliko npr. elemenata ima "grupa", bez da se kaže o kojoj se grupi radi.
[ kandorus @ 04.01.2012. 22:45 ] @
Da li hoćeš da kažeš da su platonisti ludi? I koliko je to "baš toliko"?
I šta znači da Gedel "nije bio toliko glup"? Pre bi se reklo da je Gedel bio izuzetno inteligentan, možda i inteligentniji od nekih koji se danas smatraju vodećim po tim sposobnostima.
Inače matematika nije prirodna nauka. Matematika je stvar dogovora i onogo što logički sledi iz polaznih premisa. Dakle veštačka kategorija.
[ nikolinv @ 06.01.2012. 12:24 ] @
Citat: kandorus: Inače matematika nije prirodna nauka. Matematika je stvar dogovora i onogo što logički sledi iz polaznih premisa. Dakle veštačka kategorija.
Znači tvoj filozofski pravac bi mogli nazvati formalizmom. Očigledno da je on danas među matematičarima preovladajući. Zašto? Pa pretpostavljam da presudan uticaj na matematičare ostavlja aksiomatski metod za većinu matematičkih teorija, a pogotovo to da su aksiomatizovane glavne grane matematike poput analize, aritmetike, geometrije ...
Naravno, ne bi trebalo umanjiti značaj Gedelovih rezultata i Koenovog dokaza nezavisnosti hipoteze kontinuuma. [ Nedeljko @ 06.01.2012. 17:28 ] @
Matematika nije samo stvar dogovora, jer onda ne bi imala nikakav sadržaj, tj. ne bi ništa tvrdila, pa ne bi bila saznajna delatnost uopšte i bila bi vrlo laka, jer papir trpi sve. Sadržaj matematike čine veze između uvedenih pojmova. Ne može se istovremeno uvesti teorija realnih brojeva, pojmovi funkcija, metričkih prostora, kompaktnosti, neprekidnosti i ravnomerne neprekidnosti onako kako se standardno uvode, a da pritom postoji neprekidna funkcija jednog kompaktnog metričkog prostora u neki metrički prostor, koja je neprekidna i nije ravnomerno neprekidna. Uz sve prethodne konvencije, poslednje nije proizvoljnost, već nužnost.
[ kandorus @ 07.01.2012. 00:21 ] @
^nikolinv
Pa ja se držim podele prirodno/veštačko onako kako je uobičajeno. Naravno, u krajnjoj instanci sve je prirodno (ne postoje vanprirodne pojave) pa je takva podela uslovna. Ako se pogledaju matematičke konstrukcije i objekti može se primetiti da su to sve "man made" kategorije (isto kao što su računari na primer) pa onda takvu oblast nazivamo "veštački" sistem/nauka.
Matematičke strukture imaju svoj značaj u matematici ali se razlikuju od kategorija koje smatramo prirodnim. Na primer pojam grupe (koja je formalizovan matematički objekat) se razlikuje od uobičajenog pojma grupe koji je usvojen na osnovu svakodnevnog iskustva. Slično je sa "prstenom", "poljem" itd.
Zato je uvodjenje matematičkih pojmova u nastavi osetljivo pitanje. Učenik mora da "uništi" ranije usvojene kategorije da bi usvojio matematičke kategorije. To donekle ograničava razvoj ličnosti. Ali činjenica je da čovek sve više živi upleten u "veštačku stvarnost" tako da se čini neophodnim doza "uvrtanja" kategorija. Gde su tu granice moraće se uključi i širi krug stručnjaka a ne samo matematičari da bi se došlo do odgovora na ta pitanja.
Slično je i sa pitanjem ove teme. Tokom studija budući nastavnik mora samo da reprodukuje matematičke činjenice tipa "skup N0 je skup prirodnih brojeva sa nulom" ili da povuče crtu na tabli i označi tačku koju nazove "nula" pa je dobio "realnu pravu". I onda se nastavnik nadje u čudu kad ga učenik upita "a šta je to nula?". Kako sad da učeniku kaže "nula je neutralni element za operaciju sabiranja"?
Dakle problem je stvoren još tokom studija. Budući nastavnik matematike usvaja razne kategorije ali se ne obučava za svoj osnovni posao a to je da prenese sadržaj matematičkih kategorija na učenika.
[ atelago @ 07.01.2012. 21:15 ] @
Citat: kandorus:
Dakle problem je stvoren još tokom studija. Budući nastavnik matematike usvaja razne kategorije ali se ne obučava za svoj osnovni posao a to je da prenese sadržaj matematičkih kategorija na učenika.
Dobro. Ja sam mislio da znam šta je nula pa se ispostavilo da ne znam i onda je moj negativan
uticaj uklonjen. To je, naravno, u redu. Ja sam sad učenik koji treba da sazna šta je ta "kategorija",
ali pošto je "problem je stvoren još tokom studija" postavlja se pitanje na koji način su ipak studenti
saznali nešto što ne umeju da prenesu na normalnu pametnu decu (sebe, naravno, isključujem pošto
nisam dete a ni dovoljno pametan pa sam, verovatno, i loš učenik).
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|