[ Everick @ 29.11.2017. 21:25 ] @
| Kvadratni koren iz -1 je i. Treći koren iz -1 je -1. Četvrti koren iz -1 je ? |
|
[ Everick @ 29.11.2017. 21:25 ] @
[ Shadowed @ 29.11.2017. 23:25 ] @
(1+i) / sqrt(2)
[ dusanboss @ 30.11.2017. 00:39 ] @
Auu bre . A ja mislio da je meni dosadno i da ne znam šta ću sa sobom.
Dodjem na MadZone i odma se utešim [ Bojan Basic @ 30.11.2017. 13:26 ] @
[ stopnarkomaniji @ 30.11.2017. 15:18 ] @
Drži se ti gorile i lava.
Kvadratni koren: http://www.wolframalpha.com/input/?i=sqrt[-1] ==> {+i,-i} Treći koren: http://www.wolframalpha.com/input/?i=%28-1%29^%281%2F3%29 ==> {-1,e^(iπ/3),e^(-iπ/3)} Četvrti koren: http://www.wolframalpha.com/input/?i=%28-1%29^%281%2F4%29 ==> {e^(iπ/4),e^(-iπ/4),e^(3iπ/4),e^(-3iπ/4)} [ Java Beograd @ 30.11.2017. 17:03 ] @
[ mjanjic @ 30.11.2017. 22:35 ] @
Postoji u matematici dva slučaja koja su suštinski različita:
 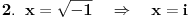 Dakle, ako se gleda rešenje kvadratne jednačine, onda ih ima dva, a ako se gleda samo vrednost korena, onda ima jedna. Ove dve jednakosti (pod 1. i 2. sa leve strane) nisu identične, tj. prva je kvadratna jednačina, a druga je samo vrednost koja se dodeljuje promenljivoj x. Za drugi izraz se ne može reći da je koren iz -1 jednako -i samo zato što jednakost važi nakon kvadriranja obe strane (čime se dobija jednakost 1.), jer se kvadriranjem upravo gubi informacija o predznaku. Zato je koren iz 4 uvek jednako 2, a nikada -2, iako je kvadrat oba broja jednak 4, a -2 se dobija jedino kao 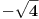 . .Zato se nakon eventualnog kvadriranja obe strane jednakosti pri rešavanju jednačina ili proveravanju jednakosti obavezno vodi računa o tome da se nakon proveri koja rešenja zadovoljavaju polaznu jednakost. [ djoka_l @ 01.12.2017. 08:50 ] @
Citat: mjanjic: Postoji u matematici dva slučaja koja su suštinski različita:  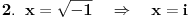 Dakle, ako se gleda rešenje kvadratne jednačine, onda ih ima dva, a ako se gleda samo vrednost korena, onda ima jedna. Ove dve jednakosti (pod 1. i 2. sa leve strane) nisu identične, tj. prva je kvadratna jednačina, a druga je samo vrednost koja se dodeljuje promenljivoj x. Za drugi izraz se ne može reći da je koren iz -1 jednako -i samo zato što jednakost važi nakon kvadriranja obe strane (čime se dobija jednakost 1.), jer se kvadriranjem upravo gubi informacija o predznaku. Zato je koren iz 4 uvek jednako 2, a nikada -2, iako je kvadrat oba broja jednak 4, a -2 se dobija jedino kao 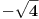 . .Zato se nakon eventualnog kvadriranja obe strane jednakosti pri rešavanju jednačina ili proveravanju jednakosti obavezno vodi računa o tome da se nakon proveri koja rešenja zadovoljavaju polaznu jednakost. Kvadratna jednačina je specijalan slučaj, možemo da posmatramo i opštije: Ako predstavimo kompleksni broj u trigonometrijskom obliku ili eksponencijalnom imamo da je 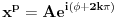 zbog periodičnosti zbog periodičnostitada su rešenja (ako postoje) oblika 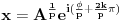 U slučaju 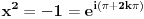 pa je pa je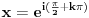 jednačina ima beskonačno mnogo rešenja, ali samo dva različita: 1 i -1 [ Bojan Basic @ 01.12.2017. 15:19 ] @
Citat: mjanjic: 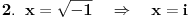 Dakle, ako se gleda rešenje kvadratne jednačine, onda ih ima dva, a ako se gleda samo vrednost korena, onda ima jedna. Baš u tome je problem: koju jednu vrednost ćeš izabrati za 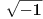 , hoće li to biti , hoće li to biti  ili ili 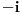 ? Ako je koren realan, onda postoji konvencija po kojoj za koren uzimamo nenegativnu vrednost, pa stoga kažemo ? Ako je koren realan, onda postoji konvencija po kojoj za koren uzimamo nenegativnu vrednost, pa stoga kažemo 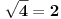 a ne a ne 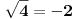 . Međutim, ako je koren kompleksan, kako u skupu kompleksnih brojeva nemamo podelu na pozitivne i negativne (niti neko adekvatno uopštenje), stoga kompleksan koren možemo posmatrati jedino kao višeznačnu funkciju. Dakle, ako hoćete bilo šta da kažete za . Međutim, ako je koren kompleksan, kako u skupu kompleksnih brojeva nemamo podelu na pozitivne i negativne (niti neko adekvatno uopštenje), stoga kompleksan koren možemo posmatrati jedino kao višeznačnu funkciju. Dakle, ako hoćete bilo šta da kažete za 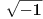 , još bi i moglo , još bi i moglo 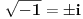 , ali nikako , ali nikako 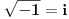 . .[ stopnarkomaniji @ 01.12.2017. 16:22 ] @
U udžbeniku iz matematike za srednju školu
jasno stoji Citat: definišimo i = √-1 Dakle, učenik se sreće sa definicijom a ne izvodjenjem. Zato neće ni razmišljati o mogućnosti da postoji više vrednosti. Otuda stalno konfliktne diskusije o vrednosti korena negativnog broja. [ Everick @ 01.12.2017. 21:41 ] @
Mislim da je vreme da se Nedeljko ovde umeša. Ipak je Nedeljko neprevaziđen po pitanju matematike ovde na forumu.
[ mjanjic @ 01.12.2017. 23:01 ] @
Ako ćemo "mak na konac", pogledajte lepo definiciju za polje kompleksnih brojeva, kao i kako se definiše imaginarna jedinica. Evo, na primer ovde: http://imft.ftn.uns.ac.rs/~vanja/old/P4.pdf
Nigde se tu ne pominje koren iz minus jedan, već skup uređenih parova realnih brojeva (a,b) sa operacijama na tom skupu (sabiranje i množenje kao binarne, kao i dve unarne operacije). Tu se lepo za par (0,1) kaže da predstavlja imaginarnu jedinicu, kao i da je (0,1)·(0,1) = -1. I gde se tu pominje koren iz minus jedan? Ono što jeste prihvatljivo je u stvari 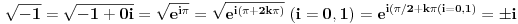 , odakle sledi da koren iz -1 ima dve vrednosti, međutim ovde se koren iz -1 posmatra kao koren kompleksnog, a ne koren realnog broja, pa zato ima dva rešenja. Zato se na višem nivou i ne govori o korenu iz -1 kao imaginarnoj jedinici, jer se radi o krenu kompleksnog broja koji ima dve vrednosti, ali se jednakost , odakle sledi da koren iz -1 ima dve vrednosti, međutim ovde se koren iz -1 posmatra kao koren kompleksnog, a ne koren realnog broja, pa zato ima dva rešenja. Zato se na višem nivou i ne govori o korenu iz -1 kao imaginarnoj jedinici, jer se radi o krenu kompleksnog broja koji ima dve vrednosti, ali se jednakost 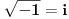 uvodi u srednjoj školi kao analogna korenu pozitivnog realnog broja, a i da bi učenici kasnije manje imali problema sa shvatanjem konjugovano-kompleksnih brojeva i sl. uvodi u srednjoj školi kao analogna korenu pozitivnog realnog broja, a i da bi učenici kasnije manje imali problema sa shvatanjem konjugovano-kompleksnih brojeva i sl.Inače, parovi konjugovano-kompleksnih brojeva su uvek rešenja kubne jednačine sa realnim koeficijentima kada je samo jedno rešenje realno, a i kvadratnih jednačina sa realnim koeficijentima koje nemaju realna rešenja (što je očigledno iz opšte formule za rešenja kada je diskriminanta negativna). [ Everick @ 03.12.2017. 14:44 ] @
Koliki je kvadratni koren iz -i?
[ Java Beograd @ 03.12.2017. 14:52 ] @
[ Bradzorf012 @ 03.12.2017. 15:40 ] @
mjanjic
Najpre si lepo objasnio u prvom javljanju, a onda si u drugom rekao da koren ima dve vrednosti. Ne može da ima dve vrednosti, jer to onda nije funkcija. Što kaže Bojan, "višeznačna funkcija", ali to onda nije funkcija. Ok, može biti da ima više vrednosti u jednoj tački, ali su onda u pitanju različite grane iste funkcije, što ovde nije slučaj. Dakle jednačina x2 = a za a >= 0 ima dva rešenja: -1 i 1, tj. √a i -√a. Šta uzeti kao √a za a < 0 je već drugo pitanje. [ Braxi @ 04.12.2017. 10:14 ] @
jaoj kad se setim kompleksne analize. Nikad vise !
[ stopnarkomaniji @ 04.12.2017. 23:14 ] @
Komrad Bradzorf
Zar se ne kaže "u jednoj tačci"? To ne znam zašto se tako kaže. Ali kad je reč o višeznačnim funkcijama onda preslikavanje F:M --> P(C) se naziva višeznačna funkcija. Ako je f: M --> C neprekidno preslikavanje i f(z) element F(z) za z element M tada je f grana višeznačne funkcije F. U tom smislu, koren je višeznačna funkcija. Jer w = z^(1/n), n element N\{1} i koren se definiše kao rešenje jednačine w^n = z stoga je F(z) = z^(1/n) višeznačna funkcija. [ Java Beograd @ 05.12.2017. 06:45 ] @
Citat: stopnarkomaniji: Zar se ne kaže "u jednoj tačci"? [ Shadowed @ 05.12.2017. 08:20 ] @
Pricao je Mjao razne gluposti.
[ stopnarkomaniji @ 05.12.2017. 08:20 ] @
Ma za te primere znam.
Samo sam hteo da čujem gramatičko obrazloženje. [ stopnarkomaniji @ 05.12.2017. 12:49 ] @
A što se ti mešaš tamo gde nisi prozvan?
Uostalom, lepo sam napisao da ne zanam misleći na to šta je gramatički ispravno. Ali ako si baš besposlen evo pitanje i tebi: "Zar se ne kaže..."? Pismeni odgovor dostaviti uz gramatičko obrazloženje. [ stopnarkomaniji @ 05.12.2017. 13:39 ] @
To što neko napiše da ne zna granatiku ne znači da je glup.
Ali ti isto tako ne znaš gramatiku inače bi već napisao obrazloženje. Dakle, ni ti ne znaš šta je ispravno a misliš da nekoga zezaš. Pre će biti da nešto lečiš. [ stopnarkomaniji @ 05.12.2017. 14:09 ] @
Dobro, kad lečiš komplekse onda je sve u redu.
[ stopnarkomaniji @ 05.12.2017. 14:35 ] @
Umišljaš da si pomogao. Pitanje je bilo gramatike a ti ne znaš odgovor. Nisi nikom pomogao pa nema druge da umišljaš da si pomogao.
Ali ako ti umišljanje pomaže da se lečiš onda nastavi da umišljaš. A sad me ispričaj jer moram da počistim štalu. Pa kad se vratim. Copyright (C) 2001-2026 by www.elitesecurity.org. All rights reserved.
|